


Next: 3.7 Fully normalized associated
Up: 3 Geoid Height, Step
Previous: 3.5 Permanent tide system
Contents
An important part of the computation is the subtraction of the
reference ellipsoid, defined by the semi-major axis of the Earth 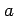 and the flattening parameter
and the flattening parameter 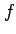 . To do so, the zonal coefficients
of the spherical harmonic gravity model
. To do so, the zonal coefficients
of the spherical harmonic gravity model
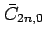 ,
,
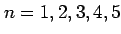 are corrected by
are corrected by
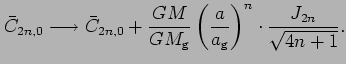 |
(20) |
The factor
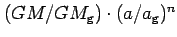 accounts for the fact that neither the gravity mass constants nor
the semi-major axes (just a scaling factor for the geopotential
model) have to be the same for geopotential model and reference
ellipsoid. In fact, very often they are not the
same.3 In general, it is sufficient to correct
the zonal coefficients
accounts for the fact that neither the gravity mass constants nor
the semi-major axes (just a scaling factor for the geopotential
model) have to be the same for geopotential model and reference
ellipsoid. In fact, very often they are not the
same.3 In general, it is sufficient to correct
the zonal coefficients
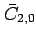 through
through
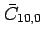 . The coefficients
. The coefficients 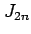 are determined from
the parameters
are determined from
the parameters 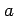 ,
, 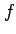 , and the angular velocity
, and the angular velocity 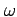 of the
Earth by an expansion (Heiskanen and Moritz, 1967, p.73, eq.2-92):
of the
Earth by an expansion (Heiskanen and Moritz, 1967, p.73, eq.2-92):
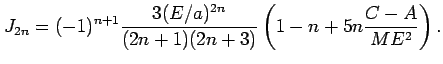 |
(21) |
This equation involves new parameters: the moments of inertia with
respect to any axis in the equatorial plane 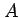 and with respect to
the axis of rotation
and with respect to
the axis of rotation 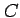 (not to be confused with the spherical
harmonic coefficients
(not to be confused with the spherical
harmonic coefficients
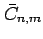 ), the total mass
), the total mass 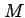 , and the linear
eccentricity
, and the linear
eccentricity
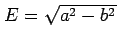 . They can be computed by
(Heiskanen and Moritz, 1967)
. They can be computed by
(Heiskanen and Moritz, 1967)
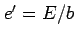 is again the second numerical eccentricity. Subtracting the
reference ellipsoid is a very sensitive operation, because two large
numbers are subtracted from each other and this is always prone to
errors. So if your coefficients
is again the second numerical eccentricity. Subtracting the
reference ellipsoid is a very sensitive operation, because two large
numbers are subtracted from each other and this is always prone to
errors. So if your coefficients 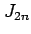 are only slightly wrong,
this will have a big effect on your solution. If you are lucky, the
precomputed values of the coefficients
are only slightly wrong,
this will have a big effect on your solution. If you are lucky, the
precomputed values of the coefficients 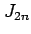 , which are in
principle defined by
, which are in
principle defined by 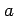 ,
, 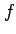 ,
, 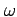 , and
, and  , are provided with
the reference ellipsoid.
, are provided with
the reference ellipsoid.



Next: 3.7 Fully normalized associated
Up: 3 Geoid Height, Step
Previous: 3.5 Permanent tide system
Contents
mlosch@awi-bremerhaven.de
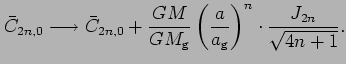
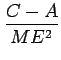
![$\displaystyle =\frac{1}{3}\left[1- \frac{2}{15}\left(\frac{me'}{q_{0}}\right)\right]$](img74.png)
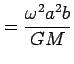
![$\displaystyle =\frac{1}{2}\left[\left(1 +\frac{3}{e'^{2}}\right)\arctan{e'} -\frac{3}{e'}\right].$](img76.png)