Mapping the solutions

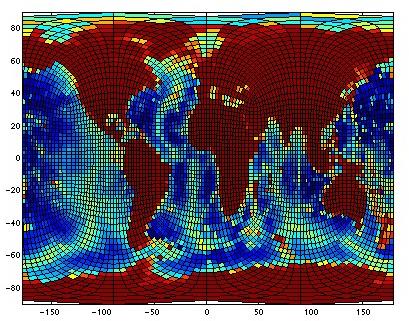
The cubic grids, like many curvilinear grids, produce unintuitive maps between physical and computational space. A conventional projection use for displaying spherical data is the mercator projection (shown below). We've drawn the grid lines of the cubic grid on which the data shown (bathymetry) was contained. It shows how the model coordinates are oriented in arbitrary physical directions making analysis more tricky. For instance, calculating a zonal average is trivial on a regular lat-lon grid but no longer so on the cubic grids.

To make life even more interesting, the most useful pattern/orientation of storage with in computer memory is unintuitive too. Below we show how the six faces of the cube are laid out in memory with their particular orientations.

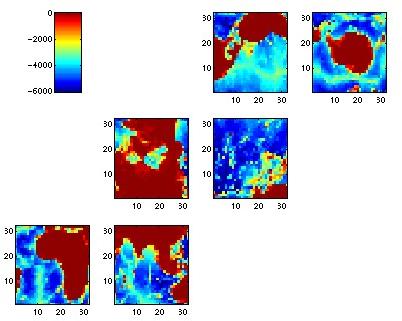The North pole is in the the center of the third tile from the bottom-left and with the Greenwich meridian pointing to the left. The South pole is the upper-left most tile with the Greenwich meridian pointing upwards. The equator spans the the two bottom most tiles from left to right and then cuts upwards across tiles four and five.