|
|
|
|




Next: 5.1.2 Reverse or adjoint
Up: 5.1 Some basic algebra
Previous: 5.1 Some basic algebra
Contents
Consider a perturbation to the input variables
 (typically a single component
(typically a single component
 ).
Their effect on the output may be obtained via the linear
approximation of the model
).
Their effect on the output may be obtained via the linear
approximation of the model  in terms of its Jacobian matrix
in terms of its Jacobian matrix
 , evaluated in the point
, evaluated in the point 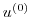 according to
according to
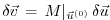 |
(5.2) |
with resulting output perturbation
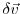 .
In components
.
In components
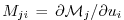 ,
it reads
,
it reads
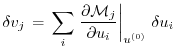 |
(5.3) |
Eq. (5.2) is the tangent linear model (TLM).
In contrast to the full nonlinear model 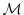 , the operator
, the operator
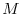 is just a matrix
which can readily be used to find the forward sensitivity of
is just a matrix
which can readily be used to find the forward sensitivity of 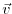 to
perturbations in
to
perturbations in  ,
but if there are very many input variables
,
but if there are very many input variables
 for
large-scale oceanographic application), it quickly becomes
prohibitive to proceed directly as in (5.2),
if the impact of each component
for
large-scale oceanographic application), it quickly becomes
prohibitive to proceed directly as in (5.2),
if the impact of each component
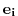 is to be assessed.
is to be assessed.




Next: 5.1.2 Reverse or adjoint
Up: 5.1 Some basic algebra
Previous: 5.1 Some basic algebra
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|