|
|
|
|




Next: 5.3.1 Code description
Up: 5. Automatic Differentiation
Previous: 5.2.5 The control variables
Contents
5.3 The gradient check package
An indispensable test to validate the gradient computed
via the adjoint is a comparison against finite difference
gradients.
The gradient check package pkg/grdchk enables such tests
in a straightforward and easy manner.
The driver routine grdchk_main is called from
the_model_main after the gradient has been computed
via the adjoint model (cf. flow chart ???).
The gradient check proceeds as follows:
The 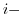 th component of the gradient
th component of the gradient
 is compared with the following finite-difference gradient:
is compared with the following finite-difference gradient:
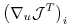 vs. 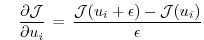
A gradient check at point  may generally considered to be successful
if the deviation of the ratio between the adjoint and the
finite difference gradient from unity is less than 1 percent,
may generally considered to be successful
if the deviation of the ratio between the adjoint and the
finite difference gradient from unity is less than 1 percent,
Subsections
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|







