|
|
|
|




Next: 7.7.4 Technical details
Up: 7.7 Potential vorticity Matlab
Previous: 7.7.2 Equations
Contents
- A_compute_potential_density.m: Compute the potential density
field. Requires the potential temperature and salinity (either total or anomalous) and
produces one output file with the potential density field (file prefix is SIGMATHETA). The routine uses densjmd95.m a Matlab counterpart of the
MITgcm built-in function to compute the density.
- B_compute_relative_vorticity.m: Compute the three components of
the relative vorticity defined in Eq. (7.1). Requires the two
horizontal velocity components and produces three output files with the three components
(files prefix are OMEGAX, OMEGAY and ZETA).
- C_compute_potential_vorticity.m: Compute the potential
vorticity without the negative ratio by the density. Two options are possible in order
to compute either the full component (term into parenthesis in
Eq. 7.3) or the planetary component (
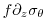 in
Eq. 7.4). Requires the relative vorticity components and the potential
density, and produces one output file with the potential vorticity (file prefix is
PV for the full term and splPV for the planetary component).
in
Eq. 7.4). Requires the relative vorticity components and the potential
density, and produces one output file with the potential vorticity (file prefix is
PV for the full term and splPV for the planetary component).
- D_compute_potential_vorticity.m: Load the field computed with
C_comp... and divide it by
 to obtain the
correct potential vorticity. Require the density field and after loading, overwrite the
file with prefix PV or splPV.
to obtain the
correct potential vorticity. Require the density field and after loading, overwrite the
file with prefix PV or splPV.
- compute_density.m: Compute the density
 from the potential
temperature and the salinity fields.
from the potential
temperature and the salinity fields.
- compute_JFz.m: Compute the surface vertical PV flux due to
frictional processes. Requires the wind stress components, density, potential density
and Ekman layer depth (all of them, except the wind stress, may be computed with the
package), and produces one output file with the PV flux
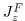 (see
Eq. 7.6) and with JFz as a prefix.
(see
Eq. 7.6) and with JFz as a prefix.
- compute_JBz.m: Compute the surface vertical PV flux due to
diabatic processes as:
which is a simplified version of the full expression given in
Eq. (7.5). Requires the net surface heat flux and the mixed layer depth
(of which an estimation can be computed with the package), and produces one output file
with the PV flux  and with JBz as a prefix.
and with JBz as a prefix.
- compute_QEk.m: Compute the horizontal heat flux due to Ekman
currents from the PV flux induced by frictional forces as:
Requires the PV flux due to frictional forces and the Ekman layer depth, and produces one
output with the heat flux and with QEk as a prefix.
- eg_main_getPV: A complete example of how to set up a master
routine able to compute everything from the package.




Next: 7.7.4 Technical details
Up: 7.7 Potential vorticity Matlab
Previous: 7.7.2 Equations
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|







