|
 |
|||||||||||
 |
|
|||||||||||
 |
 |
|||||||||||
|
Next: 2.9 Non-hydrostatic formulation Up: 2. Discretization and Algorithm Previous: 2.7 Synchronous time-stepping: variables Contents
|
|
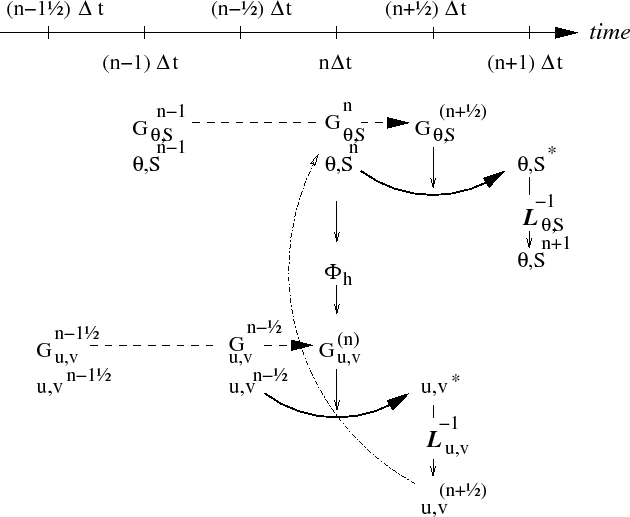
For well stratified problems, internal gravity waves may be the limiting process for determining a stable time-step. In the circumstance, it is more efficient to stagger in time the thermodynamic variables with the flow variables. Fig. 2.7 illustrates the staggering and algorithm. The key difference between this and Fig. 2.5 is that the thermodynamic variables are solved after the dynamics, using the recently updated flow field. This essentially allows the gravity wave terms to leap-frog in time giving second order accuracy and more stability.
The essential change in the staggered algorithm is that the
thermodynamics solver is delayed from half a time step,
allowing the use of the most recent velocities to compute
the advection terms. Once the thermodynamics fields are
updated, the hydrostatic pressure is computed
to step forward the dynamics.
Note that the pressure gradient must also be taken out of the
Adams-Bashforth extrapolation. Also, retaining the integer time-levels,
![]() and
and ![]() , does not give a user the sense of where variables are
located in time. Instead, we re-write the entire algorithm,
2.29 to 2.40, annotating the
position in time of variables appropriately:
, does not give a user the sense of where variables are
located in time. Instead, we re-write the entire algorithm,
2.29 to 2.40, annotating the
position in time of variables appropriately:
The corresponding calling tree is given in 2.8. The staggered algorithm is activated with the run-time flag staggerTimeStep=.TRUE. in parameter file data, namelist PARM01.

|
The only difficulty with this approach is apparent in equation
2.49 and illustrated by the dotted arrow
connecting
![]() with
with
![]() . The flow used to advect
tracers around is not naturally located in time. This could be avoided
by applying the Adams-Bashforth extrapolation to the tracer field
itself and advecting that around but this approach is not yet
available. We're not aware of any detrimental effect of this
feature. The difficulty lies mainly in interpretation of what
time-level variables and terms correspond to.
. The flow used to advect
tracers around is not naturally located in time. This could be avoided
by applying the Adams-Bashforth extrapolation to the tracer field
itself and advecting that around but this approach is not yet
available. We're not aware of any detrimental effect of this
feature. The difficulty lies mainly in interpretation of what
time-level variables and terms correspond to.
Next: 2.9 Non-hydrostatic formulation Up: 2. Discretization and Algorithm Previous: 2.7 Synchronous time-stepping: variables Contents mitgcm-support@mitgcm.org