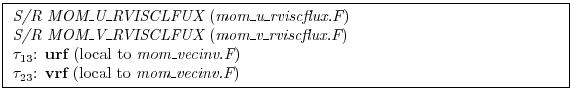|
 |
|||||||||||
 |
|
|||||||||||
 |
 |
|||||||||||
|
Next: 2.16 Tracer equations Up: 2.15 Vector invariant momentum Previous: 2.15.7 Horizontal dissipation Contents 2.15.8 Vertical dissipation
Currently, this is exactly the same code as the flux form equations.
represents the general discrete form of the vertical dissipation terms.
In the interior the vertical stresses are discretized:
mitgcm-support@mitgcm.org |
|||||||||||||||||||