|
|
|
|




Next: 2.17.1 Centered second order
Up: 2. Discretization and Algorithm
Previous: 2.16.1 Time-stepping of tracers:
Contents
2.17 Linear advection schemes
Figure 2.13:
Comparison of 1-D advection schemes. Courant number is 0.05 with 60
points and solutions are shown for T=1 (one complete period).
a) Shows the upwind biased schemes; first order upwind, DST3,
third order upwind and second order upwind.
b) Shows the centered schemes; Lax-Wendroff, DST4, centered second order,
centered fourth order and finite volume fourth order.
c) Shows the second order flux limiters: minmod, Superbee,
MC limiter and the van Leer limiter.
d) Shows the DST3 method with flux limiters due to Sweby with
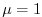 ,
,
 and a fourth order DST method with Sweby limiter,
and a fourth order DST method with Sweby limiter,
 .
.

|
Figure 2.14:
Comparison of 1-D advection schemes. Courant number is 0.89 with 60
points and solutions are shown for T=1 (one complete period).
a) Shows the upwind biased schemes; first order upwind and DST3.
Third order upwind and second order upwind are unstable at this Courant number.
b) Shows the centered schemes; Lax-Wendroff, DST4. Centered second order,
centered fourth order and finite volume fourth order and unstable at this
Courant number.
c) Shows the second order flux limiters: minmod, Superbee,
MC limiter and the van Leer limiter.
d) Shows the DST3 method with flux limiters due to Sweby with
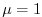 ,
,
 and a fourth order DST method with Sweby limiter,
and a fourth order DST method with Sweby limiter,
 .
.

|
The advection schemes known as centered second order, centered fourth
order, first order upwind and upwind biased third order are known as
linear advection schemes because the coefficient for interpolation of
the advected tracer are linear and a function only of the flow, not
the tracer field it self. We discuss these first since they are most
commonly used in the field and most familiar.
Subsections




Next: 2.17.1 Centered second order
Up: 2. Discretization and Algorithm
Previous: 2.16.1 Time-stepping of tracers:
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|