|
|
|
|




Next: 2.21.1 Eddy Viscosity
Up: 2. Discretization and Algorithm
Previous: 2.20.1 SHAP Diagnostics
Contents
2.21 Nonlinear Viscosities for Large Eddy Simulation
In Large Eddy Simulations (LES), a turbulent closure needs to be
provided that accounts for the effects of subgridscale motions on the
large scale. With sufficiently powerful computers, we could resolve
the entire flow down to the molecular viscosity scales
(
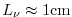 ). Current computation allows perhaps
four decades to be resolved, so the largest problem computationally
feasible would be about 10m. Most oceanographic problems are much
larger in scale, so some form of LES is required, where only the
largest scales of motion are resolved, and the subgridscale's effects
on the large-scale are parameterized.
). Current computation allows perhaps
four decades to be resolved, so the largest problem computationally
feasible would be about 10m. Most oceanographic problems are much
larger in scale, so some form of LES is required, where only the
largest scales of motion are resolved, and the subgridscale's effects
on the large-scale are parameterized.
To formalize this process, we can introduce a filter over the
subgridscale L:
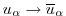 and
and
 . This filter has some intrinsic length and time
scales, and we assume that the flow at that scale can be characterized
with a single velocity scale (
. This filter has some intrinsic length and time
scales, and we assume that the flow at that scale can be characterized
with a single velocity scale (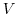 ) and vertical buoyancy gradient
(
) and vertical buoyancy gradient
( ). The filtered equations of motion in a local Mercator
projection about the gridpoint in question (see Appendix for notation
and details of approximation) are:
). The filtered equations of motion in a local Mercator
projection about the gridpoint in question (see Appendix for notation
and details of approximation) are:
Tildes denote multiplication by
 to account
for converging meridians.
to account
for converging meridians.
The ocean is usually turbulent, and an operational definition of
turbulence is that the terms in parentheses (the 'eddy' terms) on the
right of (2.206) are of comparable magnitude to the terms on
the left-hand side. The terms proportional to the inverse of Re,
instead, are many orders of magnitude smaller than all of the other
terms in virtually every oceanic application.
Subsections




Next: 2.21.1 Eddy Viscosity
Up: 2. Discretization and Algorithm
Previous: 2.20.1 SHAP Diagnostics
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|







