|
|
|
|



Next: 2.10.2 The finite volume
Up: 2.10 Spatial discretization of
Previous: 2.10 Spatial discretization of
Contents
The notations we use to describe the discrete formulation
of the model are summarized hereafter:
general notation:
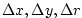 grid spacing in X,Y,R directions. grid spacing in X,Y,R directions.
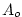 : Area of the face orthogonal to "o" direction (o=u,v,w ...). : Area of the face orthogonal to "o" direction (o=u,v,w ...).
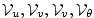 :
Volume of the grid box surrounding :
Volume of the grid box surrounding
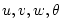 point; point;
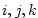 : current index relative to X,Y,R directions; : current index relative to X,Y,R directions;
basic operator:
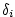 : :
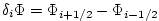
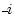 : :
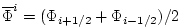
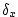 : :
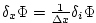
 = gradient operator : = gradient operator :
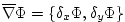
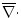 = divergence operator : = divergence operator :
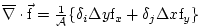
 = Laplacian operator : = Laplacian operator :
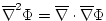
mitgcm-support@dev.mitgcm.org
| Copyright © 2002
Massachusetts Institute of Technology |
 |
|