2.16 Linear advection schemes

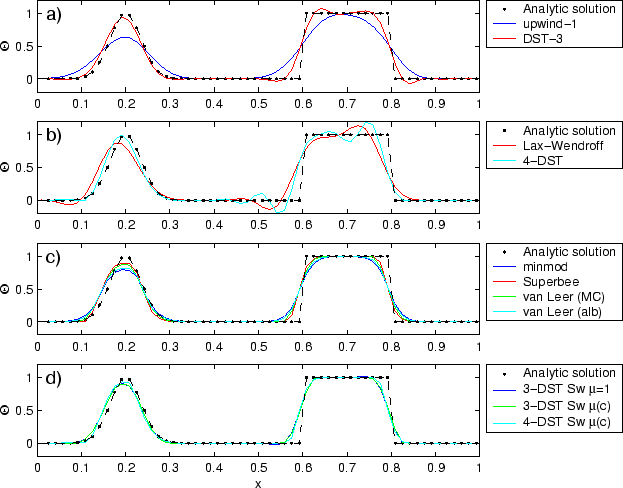
Figure 2.12: Comparison of 1-D advection schemes. Courant number is 0.05 with 60 points and solutions are shown for T=1 (one complete period). a) Shows the upwind biased schemes; first order upwind, DST3, third order upwind and second order upwind. b) Shows the centered schemes; Lax-Wendroff, DST4, centered second order, centered fourth order and finite volume fourth order. c) Shows the second order flux limiters: minmod, Superbee, MC limiter and the van Leer limiter. d) Shows the DST3 method with flux limiters due to Sweby with 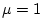, 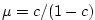and a fourth order DST method with Sweby limiter, .

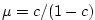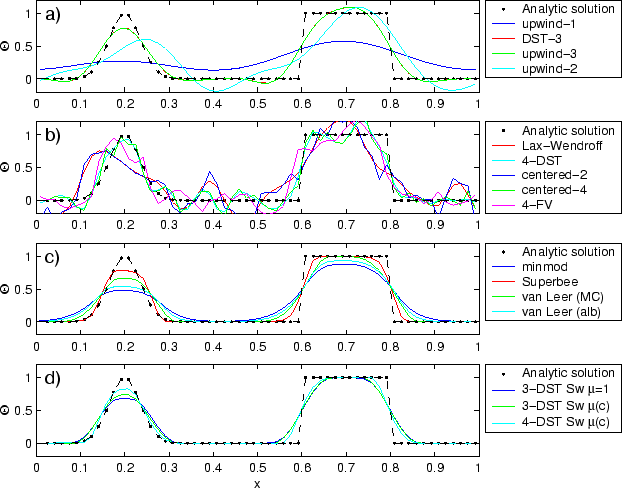Figure 2.13: Comparison of 1-D advection schemes. Courant number is 0.89 with 60 points and solutions are shown for T=1 (one complete period). a) Shows the upwind biased schemes; first order upwind and DST3. Third order upwind and second order upwind are unstable at this Courant number. b) Shows the centered schemes; Lax-Wendroff, DST4. Centered second order, centered fourth order and finite volume fourth order and unstable at this Courant number. c) Shows the second order flux limiters: minmod, Superbee, MC limiter and the van Leer limiter. d) Shows the DST3 method with flux limiters due to Sweby with 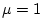, 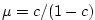and a fourth order DST method with Sweby limiter, .

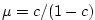The advection schemes known as centered second order, centered fourth order, first order upwind and upwind biased third order are known as linear advection schemes because the coefficient for interpolation of the advected tracer are linear and a function only of the flow, not the tracer field it self. We discuss these first since they are most commonly used in the field and most familiar.

• 2.16.1 Centered second order advection-diffusion
• 2.16.2 Third order upwind bias advection
• 2.16.3 Centered fourth order advection
• 2.16.4 First order upwind advection

Copyright © 2002 Massachusetts Institute of Technology