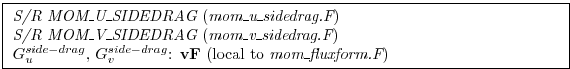Home Contact Us Site Map  
 
       
    next up previous contents
Next: 2.14.6 Vertical dissipation Up: 2.14 Flux-form momentum equations Previous: 2.14.4 Non-hydrostatic metric terms   Contents

2.14.5 Lateral dissipation

Historically, we have represented the SGS Reynolds stresses as simply down gradient momentum fluxes, ignoring constraints on the stress tensor such as symmetry.

$\displaystyle {\cal A}_w \Delta r_f h_w G_u^{h-diss}$ $\displaystyle =$ $\displaystyle \delta_i \Delta y_f \Delta r_f h_c \tau_{11} + \delta_j \Delta x_v \Delta r_f h_\zeta \tau_{12}$ (2.124)
$\displaystyle {\cal A}_s \Delta r_f h_s G_v^{h-diss}$ $\displaystyle =$ $\displaystyle \delta_i \Delta y_u \Delta r_f h_\zeta \tau_{21} + \delta_j \Delta x_f \Delta r_f h_c \tau_{22}$ (2.125)

The lateral viscous stresses are discretized:

$\displaystyle \tau_{11}$ $\displaystyle =$ $\displaystyle A_h c_{11\Delta}(\varphi) \frac{1}{\Delta x_f} \delta_i u -A_4 c_{11\Delta^2}(\varphi) \frac{1}{\Delta x_f} \delta_i \nabla^2 u$ (2.126)
$\displaystyle \tau_{12}$ $\displaystyle =$ $\displaystyle A_h c_{12\Delta}(\varphi) \frac{1}{\Delta y_u} \delta_j u -A_4 c_{12\Delta^2}(\varphi)\frac{1}{\Delta y_u} \delta_j \nabla^2 u$ (2.127)
$\displaystyle \tau_{21}$ $\displaystyle =$ $\displaystyle A_h c_{21\Delta}(\varphi) \frac{1}{\Delta x_v} \delta_i v -A_4 c_{21\Delta^2}(\varphi) \frac{1}{\Delta x_v} \delta_i \nabla^2 v$ (2.128)
$\displaystyle \tau_{22}$ $\displaystyle =$ $\displaystyle A_h c_{22\Delta}(\varphi) \frac{1}{\Delta y_f} \delta_j v -A_4 c_{22\Delta^2}(\varphi) \frac{1}{\Delta y_f} \delta_j \nabla^2 v$ (2.129)

where the non-dimensional factors $ c_{lm\Delta^n}(\varphi), \{l,m,n\} \in \{1,2\}$ define the ``cosine'' scaling with latitude which can be applied in various ad-hoc ways. For instance, $ c_{11\Delta} = c_{21\Delta} = (\cos{\varphi})^{3/2}$ , $ c_{12\Delta}=c_{22\Delta}=1$ would represent the an-isotropic cosine scaling typically used on the ``lat-lon'' grid for Laplacian viscosity.

It should be noted that despite the ad-hoc nature of the scaling, some scaling must be done since on a lat-lon grid the converging meridians make it very unlikely that a stable viscosity parameter exists across the entire model domain.

The Laplacian viscosity coefficient, $ A_h$ (viscAh), has units of $ m^2 s^{-1}$ . The bi-harmonic viscosity coefficient, $ A_4$ (viscA4), has units of $ m^4 s^{-1}$ .

\fbox{ \begin{minipage}{4.75in} {\em S/R MOM\_U\_XVISCFLUX} ({\em mom\_u\_xviscf... ...tau_{22}$: {\bf vF}, {\bf v4F} (local to {\em mom\_fluxform.F}) \end{minipage} }

Two types of lateral boundary condition exist for the lateral viscous terms, no-slip and free-slip.

The free-slip condition is most convenient to code since it is equivalent to zero-stress on boundaries. Simple masking of the stress components sets them to zero. The fractional open stress is properly handled using the lopped cells.

The no-slip condition defines the normal gradient of a tangential flow such that the flow is zero on the boundary. Rather than modify the stresses by using complicated functions of the masks and ``ghost'' points (see Adcroft and Marshall [1998]) we add the boundary stresses as an additional source term in cells next to solid boundaries. This has the advantage of being able to cope with ``thin walls'' and also makes the interior stress calculation (code) independent of the boundary conditions. The ``body'' force takes the form:

$\displaystyle G_u^{side-drag}$ $\displaystyle =$ $\displaystyle \frac{4}{\Delta z_f} \overline{ (1-h_\zeta) \frac{\Delta x_v}{\De... ...t( A_h c_{12\Delta}(\varphi) u - A_4 c_{12\Delta^2}(\varphi) \nabla^2 u \right)$ (2.130)
$\displaystyle G_v^{side-drag}$ $\displaystyle =$ $\displaystyle \frac{4}{\Delta z_f} \overline{ (1-h_\zeta) \frac{\Delta y_u}{\De... ...t( A_h c_{21\Delta}(\varphi) v - A_4 c_{21\Delta^2}(\varphi) \nabla^2 v \right)$ (2.131)

In fact, the above discretization is not quite complete because it assumes that the bathymetry at velocity points is deeper than at neighboring vorticity points, e.g. $ 1-h_w < 1-h_\zeta$

\fbox{ \begin{minipage}{4.75in} {\em S/R MOM\_U\_SIDEDRAG} ({\em mom\_u\_sidedra... ...$, $G_v^{side-drag}$: {\bf vF} (local to {\em mom\_fluxform.F}) \end{minipage} }

next up previous contents
Next: 2.14.6 Vertical dissipation Up: 2.14 Flux-form momentum equations Previous: 2.14.4 Non-hydrostatic metric terms   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2018-01-23