|
|
|
|




Next: 3.6.2 Parameters: Equation of
Up: 3.6 Customizing MITgcm
Previous: 3.6 Customizing MITgcm
Contents
- dimensions
-
The number of points in the x, y, and r directions are represented
by the variables sNx, sNy and Nr
respectively which are declared and set in the file
model/inc/SIZE.h. (Again, this assumes a mono-processor
calculation. For multiprocessor calculations see the section on
parallel implementation.)
- grid
-
Three different grids are available: cartesian, spherical polar, and
curvilinear (which includes the cubed sphere). The grid is set
through the logical variables usingCartesianGrid,
usingSphericalPolarGrid, and usingCurvilinearGrid.
In the case of spherical and curvilinear grids, the southern
boundary is defined through the variable ygOrigin which
corresponds to the latitude of the southern most cell face (in
degrees). The resolution along the x and y directions is controlled
by the 1D arrays delx and dely (in meters in the
case of a cartesian grid, in degrees otherwise). The vertical grid
spacing is set through the 1D array delz for the ocean (in
meters) or delp for the atmosphere (in Pa). The variable
Ro_SeaLevel represents the standard position of Sea-Level
in ``R'' coordinate. This is typically set to 0m for the ocean
(default value) and 10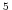 Pa for the atmosphere. For the
atmosphere, also set the logical variable groundAtK1 to
'.TRUE.' which puts the first level (k=1) at the lower
boundary (ground).
Pa for the atmosphere. For the
atmosphere, also set the logical variable groundAtK1 to
'.TRUE.' which puts the first level (k=1) at the lower
boundary (ground).
For the cartesian grid case, the Coriolis parameter 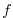 is set
through the variables f0 and beta which correspond
to the reference Coriolis parameter (in s
is set
through the variables f0 and beta which correspond
to the reference Coriolis parameter (in s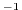 ) and
) and
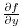 (in m
(in m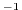 s
s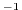 ) respectively.
If beta is set to a nonzero value, f0 is the
value of
) respectively.
If beta is set to a nonzero value, f0 is the
value of 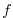 at the southern edge of the domain.
at the southern edge of the domain.
- topography - full and partial cells
-
The domain bathymetry is read from a file that contains a 2D (x,y)
map of depths (in m) for the ocean or pressures (in Pa) for the
atmosphere. The file name is represented by the variable
bathyFile. The file is assumed to contain binary numbers
giving the depth (pressure) of the model at each grid cell, ordered
with the x coordinate varying fastest. The points are ordered from
low coordinate to high coordinate for both axes. The model code
applies without modification to enclosed, periodic, and double
periodic domains. Periodicity is assumed by default and is
suppressed by setting the depths to 0m for the cells at the limits
of the computational domain (note: not sure this is the case for the
atmosphere). The precision with which to read the binary data is
controlled by the integer variable readBinaryPrec which can
take the value 32 (single precision) or 64 (double
precision). See the matlab program gendata.m in the
input directories under verification to see how
the bathymetry files are generated for the case study experiments.
To use the partial cell capability, the variable hFacMin
needs to be set to a value between 0 and 1 (it is set to 1 by
default) corresponding to the minimum fractional size of the cell.
For example if the bottom cell is 500m thick and hFacMin is
set to 0.1, the actual thickness of the cell (i.e. used in the code)
can cover a range of discrete values 50m apart from 50m to 500m
depending on the value of the bottom depth (in bathyFile)
at this point.
Note that the bottom depths (or pressures) need not coincide with
the models levels as deduced from delz or delp.
The model will interpolate the numbers in bathyFile so that
they match the levels obtained from delz or delp
and hFacMin.
(Note: the atmospheric case is a bit more complicated than what is
written here I think. To come soon...)
- time-discretization
-
The time steps are set through the real variables deltaTMom
and deltaTtracer (in s) which represent the time step for
the momentum and tracer equations, respectively. For synchronous
integrations, simply set the two variables to the same value (or you
can prescribe one time step only through the variable
deltaT). The Adams-Bashforth stabilizing parameter is set
through the variable abEps (dimensionless). The stagger
baroclinic time stepping can be activated by setting the logical
variable staggerTimeStep to '.TRUE.'.




Next: 3.6.2 Parameters: Equation of
Up: 3.6 Customizing MITgcm
Previous: 3.6 Customizing MITgcm
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2011-01-09 |
 |
|