3.6.3 Parameters: Momentum equations

In this section, we only focus for now on the parameters that you are likely to change, i.e. the ones relative to forcing and dissipation for example. The details relevant to the vector-invariant form of the equations and the various advection schemes are not covered for the moment. We assume that you use the standard form of the momentum equations (i.e. the flux-form) with the default advection scheme. Also, there are a few logical variables that allow you to turn on/off various terms in the momentum equation. These variables are called momViscosity, momAdvection, momForcing, useCoriolis, momPressureForcing, momStepping and metricTerms and are assumed to be set to '.TRUE.' here. Look at the file model/inc/PARAMS.h for a precise definition of these variables.

initialization

The initial horizontal velocity components can be specified from binary files uVelInitFile and vVelInitFile. These files should contain 3D data ordered in an (x,y,r) fashion with k=1 as the first vertical level (surface level). If no file names are provided, the velocity is initialised to zero. The initial vertical velocity is always derived from the horizontal velocity using the continuity equation, even in the case of non-hydrostatic simulation (see, e.g.: tutorial_deep_convection/input/data).

In the case of a restart (from the end of a previous simulation), the velocity field is read from a pickup file (see section on simulation control parameters) and the initial velocity files are ignored.

forcing

This section only applies to the ocean. You need to generate wind-stress data into two files zonalWindFile and meridWindFile corresponding to the zonal and meridional components of the wind stress, respectively (if you want the stress to be along the direction of only one of the model horizontal axes, you only need to generate one file). The format of the files is similar to the bathymetry file. The zonal (meridional) stress data are assumed to be in Pa and located at U-points (V-points). As for the bathymetry, the precision with which to read the binary data is controlled by the variable readBinaryPrec. See the matlab program gendata.m in the input directories under verification to see how simple analytical wind forcing data are generated for the case study experiments.

There is also the possibility of prescribing time-dependent periodic forcing. To do this, concatenate the successive time records into a single file (for each stress component) ordered in a (x,y,t) fashion and set the following variables: periodicExternalForcing to '.TRUE.', externForcingPeriod to the period (in s) of which the forcing varies (typically 1 month), and externForcingCycle to the repeat time (in s) of the forcing (typically 1 year - note: externForcingCycle must be a multiple of externForcingPeriod). With these variables set up, the model will interpolate the forcing linearly at each iteration.

dissipation

The lateral eddy viscosity coefficient is specified through the variable viscAh (in m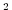 s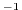 ). The vertical eddy viscosity coefficient is specified through the variable viscAz (in m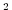 s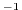 ) for the ocean and viscAp (in Pa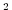 s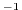 ) for the atmosphere. The vertical diffusive fluxes can be computed implicitly by setting the logical variable implicitViscosity to '.TRUE.'. In addition, biharmonic mixing can be added as well through the variable viscA4 (in m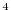 s ). 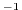On a spherical polar grid, you might also need to set the variable cosPower which is set to 0 by default and which represents the power of cosine of latitude to multiply viscosity. Slip or no-slip conditions at lateral and bottom boundaries are specified through the logical variables no_slip_sides and no_slip_bottom. If set to '.FALSE.', free-slip boundary conditions are applied. If no-slip boundary conditions are applied at the bottom, a bottom drag can be applied as well. Two forms are available: linear (set the variable bottomDragLinear in m/s) and quadratic (set the variable bottomDragQuadratic, dimensionless).

The Fourier and Shapiro filters are described elsewhere.

C-D scheme

If you run at a sufficiently coarse resolution, you will need the C-D scheme for the computation of the Coriolis terms. The variable tauCD, which represents the C-D scheme coupling timescale (in s) needs to be set.

calculation of pressure/geopotential

First, to run a non-hydrostatic ocean simulation, set the logical variable nonHydrostatic to '.TRUE.'. The pressure field is then inverted through a 3D elliptic equation. (Note: this capability is not available for the atmosphere yet.) By default, a hydrostatic simulation is assumed and a 2D elliptic equation is used to invert the pressure field. The parameters controlling the behaviour of the elliptic solvers are the variables cg2dMaxIters and cg2dTargetResidual for the 2D case and cg3dMaxIters and cg3dTargetResidual for the 3D case. You probably won't need to alter the default values (are we sure of this?).

For the calculation of the surface pressure (for the ocean) or surface geopotential (for the atmosphere) you need to set the logical variables rigidLid and implicitFreeSurface (set one to '.TRUE.' and the other to '.FALSE.' depending on how you want to deal with the ocean upper or atmosphere lower boundary).

Copyright © 2006 Massachusetts Institute of Technology

Last update 2011-01-09