|
|
|
|



Next: 3.9.2 Discrete Numerical Configuration
Up: 3.9 Barotropic Gyre MITgcm
Previous: 3.9 Barotropic Gyre MITgcm
Contents
The model is configured in hydrostatic form. The implicit free surface form of the
pressure equation described in Marshall et. al Marshall et al. [1997b] is
employed.
A horizontal Laplacian operator
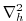 provides viscous
dissipation. The wind-stress momentum input is added to the momentum equation
for the ``zonal flow'',
provides viscous
dissipation. The wind-stress momentum input is added to the momentum equation
for the ``zonal flow'', 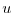 . Other terms in the model
are explicitly switched off for this experiment configuration (see section
3.9.3 ), yielding an active set of equations solved
in this configuration as follows
. Other terms in the model
are explicitly switched off for this experiment configuration (see section
3.9.3 ), yielding an active set of equations solved
in this configuration as follows
where 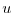 and
and 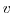 and the
and the 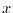 and
and 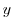 components of the
flow vector
components of the
flow vector 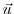 .
.
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2011-01-09 |
 |
|