|
|
|
|



Next: 3.11.2 Introducing a tracer
Up: 3.11 Gyre Advection Example
Previous: 3.11 Gyre Advection Example
Contents
In general, the tracer problem we want to solve can be written
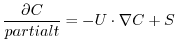 |
(3.30) |
where 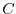 is the tracer concentration in a model cell,
is the tracer concentration in a model cell, 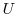 is the model three-dimensional
flow field (
is the model three-dimensional
flow field ( 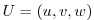 ). In (3.30)
). In (3.30) 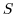 represents source, sink
and tendency terms not associated with advective transport. Example of terms in
represents source, sink
and tendency terms not associated with advective transport. Example of terms in 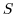 include
(i) air-sea fluxes for a dissolved gas, (ii) biological grazing and growth terms (for a
biogeochemical problem) or (iii) convective mixing and other sub-grid parameterizations of
mixing. In this section we are primarily concerned with
include
(i) air-sea fluxes for a dissolved gas, (ii) biological grazing and growth terms (for a
biogeochemical problem) or (iii) convective mixing and other sub-grid parameterizations of
mixing. In this section we are primarily concerned with
- how to introduce the tracer term,
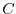 , into an integration
, into an integration
- the different discretized forms of
the
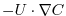 term that are available
term that are available
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2011-01-09 |
 |
|







