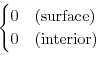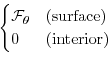3.15.2 Equations solved

The model is configured in nonhydrostatic form, that is, all terms in the Navier Stokes equations are retained and the pressure field is found, subject to appropriate bounday condintions, through inversion of a three-dimensional elliptic equation.

The implicit free surface form of the pressure equation described in Marshall et. al Marshall et al. [1997b] is employed. A horizontal Laplacian operator $\nabla_{h}^2$ provides viscous dissipation. The thermodynamic forcing appears as a sink in the potential temperature, $\theta$ , equation (3.81). This produces a set of equations solved in this configuration as follows:

$\displaystyle \frac{Du}{Dt} - fv + \frac{1}{\rho}\frac{\partial p^{'}}{\parti... ...h}\nabla_{h}u - \frac{\partial}{\partial z}A_{z}\frac{\partial u}{\partial z}$	$\displaystyle =$	$\begin{displaymath}\begin{cases} 0 & \text{(surface)} \\ 0 & \text{(interior)} \end{cases}\end{displaymath}$	(3.77)
$\displaystyle \frac{Dv}{Dt} + fu + \frac{1}{\rho}\frac{\partial p^{'}}{\parti... ...h}\nabla_{h}v - \frac{\partial}{\partial z}A_{z}\frac{\partial v}{\partial z}$	$\displaystyle =$	$\begin{displaymath}\begin{cases} 0 & \text{(surface)} \\ 0 & \text{(interior)} \end{cases}\end{displaymath}$	(3.78)
$\displaystyle \frac{Dw}{Dt} + g \frac{\rho^{'}}{\rho} + \frac{1}{\rho}\frac{\... ...h}\nabla_{h}w - \frac{\partial}{\partial z}A_{z}\frac{\partial w}{\partial z}$	$\displaystyle =$	$\begin{displaymath}\begin{cases} 0 & \text{(surface)} \\ 0 & \text{(interior)} \end{cases}\end{displaymath}$	(3.79)
$\displaystyle \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} +$	$\displaystyle =$	0	(3.80)
$\displaystyle \frac{D\theta}{Dt} - \nabla_{h}\cdot K_{h}\nabla_{h}\theta - \frac{\partial}{\partial z}K_{z}\frac{\partial\theta}{\partial z}$	$\displaystyle =$	$\begin{displaymath}\begin{cases} {\cal F}_\theta & \text{(surface)} \\ 0 & \text{(interior)} \end{cases}\end{displaymath}$	(3.81)

where $u=\frac{Dx}{Dt}$ , $v=\frac{Dy}{Dt}$ and $w=\frac{Dz}{Dt}$ are the components of the flow vector in directions

and

. The pressure is diagnosed through inversion (subject to appropriate boundary conditions) of a 3-D elliptic equation derived from the divergence of the momentum equations and continuity (see section 1.3.6).