

Next: 6.9 Generic Advection/Diffusion
Up: 6. Physical Parameterization and
Previous: 6.7 Sea Ice Package:
Contents
6.8 Bulk Formula Package
author: Stephanie Dutkiewicz
Instead of forcing the model with heat and fresh water flux data,
this package calculates these fluxes using the changing sea surface
temperature. We need to read in some atmospheric data:
air temperature, air humidity, down shortwave radiation,
down longwave radiation, precipitation, wind speed.
The current setup also reads in wind stress, but this
can be changed so that the stresses are calculated from the
wind speed.
The current setup requires that there is the thermodynamic-seaice package
(pkg/thsice, also refered below as seaice)
is also used. It would be useful though to have it also
setup to run with some very simple parametrization of the sea ice.
The heat and fresh water fluxes are calculated in bulkf_forcing.F
called from forward_step.F. These fluxes are used over open water,
fluxes over seaice are recalculated in the sea-ice package.
Before the call to bulkf_forcing.F we call
bulkf_fields_load.F to find the current atmospheric conditions.
The only other changes to the model code come from the initializing
and writing diagnostics of these fluxes.
subroutine BULKF_FIELDS_LOAD
Here we find the atmospheric data needed for the bulk formula
calculations. These are read in at periodic intervals and
values are interpolated to the current time. The data file names
come from data.blk. The values that can be read in are:
air temperature, air humidity, precipitation,
down solar radiation, down long
wave radiation, zonal and meridional wind speeds, total wind
speed, net heat flux, net freshwater forcing, cloud cover,
snow fall, zonal and meridional wind stresses, and SST and SSS
used for relaxation terms.
Not all these files are necessary or used. For instance cloud
cover and snow fall are not used in the current bulk formula
calculation. If total wind speed is not supplied, wind speed
is calculate from the zonal and meridional components. If
wind stresses are not read in, then the stresses are calculated
from the wind speed. Net heat flux and net freshwater can be
read in and used over open ocean instead of the bulk formula
calculations (but over seaice the bulkf formula is always
used). This is "hardwired" into bulkf_forcing and
the "ch" in the variable names suggests that this is "cheating".
SST and SSS need to be read in if there is any relaxation used.
subroutine BULKF_FORCING
In bulkf_forcing.F, we calculate heat and fresh water
fluxes (and wind stress, if necessary) for each grid cell.
First we determine if the grid cell is open water or seaice
and this information is carried by iceornot. There is
a provision here for a different designation if there is
snow cover (but currently this does not make any difference).
We then call bulkf_formula_lanl.F which provides
values for: up long wave radiation, latent and sensible heat
fluxes, the derivative of these three with respect to surface
temperature, wind stress, evaporation.
Net long wave radiation is calculated from the combination
of the down long wave read in and the up long wave calculated.
We then find the albedo of the surface - with a call to
sfc_albedo if there is sea-ice (see the seaice package
for information on the subroutine). If the grid cell is open
ocean the albedo is set as 0.1. Note that this is a parameter
that can be used to tune the results. The net short wave
radiation is then the down shortwave radiation minus the
amount reflected.
If the wind stress needed to be calculated in bulkf_formula_lanl.F,
it was calculated to grid cell center points, so in bulkf_forcing.F
we regrid to u and v points. We let the model know
if it has read in stresses or calculated stresses by the switch
readwindstress which is can be set in data.blk, and defaults
to .TRUE..
We then calculate Qnet and EmPmR that will be used
as the fluxes over the open ocean. There is a provision for
using runoff. If we are "cheating" and using observed fluxes
over the open ocean, then there is a provision here to
use read in Qnet and EmPmR.
The final call is to calculate averages of the terms found
in this subroutine.
subroutine BULKF_FORMULA_LANL
This is the main program of the package where the
heat fluxes and freshwater fluxes over ice and
open water are calculated. Note that this subroutine
is also called from the seaice package during the
iterations to find the ice surface temperature.
Latent heat ( ) used in this subroutine
depends on the state of the surface: vaporization for
open water, fusion and vaporization for ice surfaces.
Air temperature is converted from Celsius to Kelvin.
If there is no wind speed ( ) used in this subroutine
depends on the state of the surface: vaporization for
open water, fusion and vaporization for ice surfaces.
Air temperature is converted from Celsius to Kelvin.
If there is no wind speed (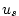 ) given, then the wind speed
is calculated from the zonal and meridional components. ) given, then the wind speed
is calculated from the zonal and meridional components.
We calculate the virtual temperature:
where 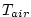 is the air temperature at is the air temperature at 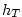 , , 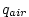 is
humidity at is
humidity at 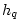 and and 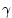 is a constant. is a constant.
The saturated vapor pressure is calculate (QQ ref):
where 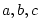 are constants, are constants, 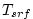 is surface temperature
and is surface temperature
and 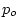 is the surface pressure. is the surface pressure.
The two values crucial for the bulk formula calculations are
the difference between air at sea surface and sea surface temperature:
where 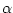 is adiabatic lapse rate and is adiabatic lapse rate and 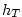 is the height
where the air temperature was taken; and the difference
between the air humidity and the saturated humidity is the height
where the air temperature was taken; and the difference
between the air humidity and the saturated humidity
We then calculate the turbulent exchange coefficients
following Bryan et al (1996) and the numerical scheme
of Hunke and Lipscombe (1998).
We estimate initial values for the exchange coefficients, 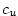 , ,
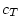 and and 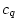 as as
where 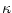 is the Von Karman constant, is the Von Karman constant, 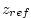 is a
reference height and is a
reference height and 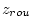 is a roughness length scale
which could be a function of type of surface, but is here set
as a constant. Turbulent scales are: is a roughness length scale
which could be a function of type of surface, but is here set
as a constant. Turbulent scales are:
We find the "integrated flux profile" for momentum and stability
if there are stable QQ conditions (
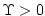 ) : ) :
and for unstable QQ conditions (
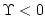 ): ):
where
and
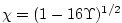 . .
The coefficients are updated through 5 iterations as:
where
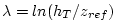 . .
We can then find the bulk formula heat fluxes:
Sensible heat flux:
Latent heat flux:
Up long wave radiation
where 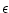 is emissivity (which can be different for
open ocean, ice and snow), is emissivity (which can be different for
open ocean, ice and snow), 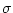 is Stefan-Boltzman constant. is Stefan-Boltzman constant.
We calculate the derivatives of the three above functions
with respect to surface temperature
And total derivative
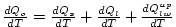 . .
If we do not read in the wind stress, it is calculated here.
Initializing subroutines
bulkf_init.F:
Set bulkf variables to zero.
bulkf_readparms.F:
Reads data.blk
Diagnostic subroutines
bulkf_ave.F:
Keeps track of means of the bulkf variables
bulkf_diags.F:
Finds averages and writes out diagnostics
Common Blocks
BULKF.h: BULKF Variables, data file names, and logicals
readwindstress and readsurface
BULKF_DIAGS.h: matrices for diagnostics: averages of fields
from bulkf_diags.F
BULKF_ICE_CONSTANTS.h:
all the parameters need by the ice model and in the bulkf formula
calculations.
Input file DATA.ICE
We read in the file names of atmospheric data used in
the bulk formula calculations. Here we can also set
the logicals: readwindstress if we read in the
wind stress rather than calculate it from the wind
speed; and readsurface to read in the surface
temperature and salinity if these will be used as
part of a relaxing term.
Important Notes
1) heat fluxes have different signs in the ocean and ice
models.
2) StartIceModel must be changed in data.ice:
1 (if starting from no ice), 0 (if using pickup.ic file).
References
Bryan F.O., B.G Kauffman, W.G. Large, P.R. Gent, 1996:
The NCAR CSM flux coupler. Technical note TN-425+STR,
NCAR.
Hunke, E.C and W.H. Lipscomb, circa 2001: CICE: the Los Alamos
Sea Ice Model Documentation and Software User's Manual.
LACC-98-16v.2.
(note: this documentation is no longer available as CICE has progressed
to a very different version 3)



Next: 6.9 Generic Advection/Diffusion
Up: 6. Physical Parameterization and
Previous: 6.7 Sea Ice Package:
Contents
mitgcm-support@dev.mitgcm.org
| Copyright © 2002
Massachusetts Institute of Technology |
 |
|





![]() ) :
) :
![]() .
.