

Next: 2.9 Variants on the
Up: 2. Discretization and Algorithm
Previous: 2.7 Staggered baroclinic time-stepping
Contents
2.8 Non-hydrostatic formulation
The non-hydrostatic formulation re-introduces the full vertical
momentum equation and requires the solution of a 3-D elliptic
equations for non-hydrostatic pressure perturbation. We still
intergrate vertically for the hydrostatic pressure and solve a 2-D
elliptic equation for the surface pressure/elevation for this reduces
the amount of work needed to solve for the non-hydrostatic pressure.
The momentum equations are discretized in time as follows:
which must satisfy the discrete-in-time depth integrated continuity,
equation 2.16 and the local continuity equation
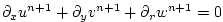 |
(2.56) |
As before, the explicit predictions for momentum are consolidated as:
but this time we introduce an intermediate step by splitting the
tendancy of the flow as follows:
Substituting into the depth integrated continuity
(equation 2.16) gives
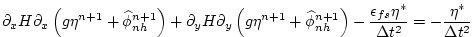 |
(2.59) |
which is approximated by equation
2.20 on the basis that i)
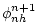 is not yet known and ii) is not yet known and ii)
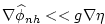 . If 2.20 is
solved accurately then the implication is that . If 2.20 is
solved accurately then the implication is that
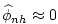 so that thet non-hydrostatic pressure field does not drive
barotropic motion. so that thet non-hydrostatic pressure field does not drive
barotropic motion.
The flow must satisfy non-divergence
(equation 2.58) locally, as well as depth
integrated, and this constraint is used to form a 3-D elliptic
equations for
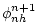 : :
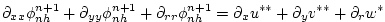 |
(2.60) |
The entire algorithm can be summarized as the sequential solution of
the following equations:
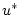 |
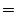 |
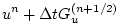 |
(2.61) |
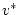 |
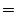 |
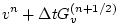 |
(2.62) |
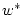 |
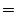 |
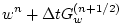 |
(2.63) |
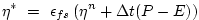 |
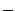 |
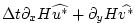 |
(2.64) |
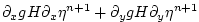 |
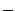 |
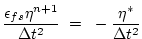 |
(2.65) |
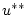 |
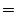 |
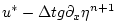 |
(2.66) |
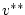 |
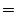 |
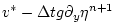 |
(2.67) |
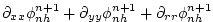 |
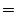 |
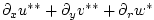 |
(2.68) |
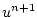 |
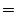 |
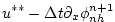 |
(2.69) |
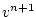 |
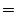 |
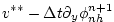 |
(2.70) |
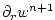 |
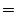 |
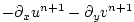 |
(2.71) |
where the last equation is solved by vertically integrating for
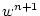 . .



Next: 2.9 Variants on the
Up: 2. Discretization and Algorithm
Previous: 2.7 Staggered baroclinic time-stepping
Contents
mitgcm-support@dev.mitgcm.org
| Copyright © 2002
Massachusetts Institute of Technology |
 |
|





![]() :
: