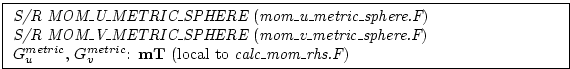|
|
|
|



Next: 2.13.4 Non-hydrostatic metric terms
Up: 2.13 Flux-form momentum equations
Previous: 2.13.2 Coriolis terms
Contents
The most commonly used coordinate system on the sphere is the
geographic system
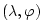 . The curvilinear nature of these
coordinates on the sphere lead to some ``metric'' terms in the
component momentum equations. Under the thin-atmosphere and
hydrostatic approximations these terms are discretized: . The curvilinear nature of these
coordinates on the sphere lead to some ``metric'' terms in the
component momentum equations. Under the thin-atmosphere and
hydrostatic approximations these terms are discretized:
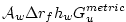 |
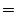 |
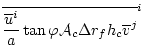 |
(2.113) |
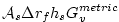 |
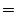 |
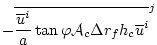 |
(2.114) |
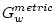 |
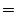 |
0 |
(2.115) |
where 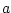 is the radius of the planet (sphericity is assumed) or the
radial distance of the particle (i.e. a function of height). It is
easy to see that this discretization satisfies all the properties of
the discrete Coriolis terms since the metric factor is the radius of the planet (sphericity is assumed) or the
radial distance of the particle (i.e. a function of height). It is
easy to see that this discretization satisfies all the properties of
the discrete Coriolis terms since the metric factor
 can be viewed as a modification of the vertical Coriolis
parameter: can be viewed as a modification of the vertical Coriolis
parameter:
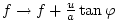 . .
However, as for the Coriolis terms, a non-energy conserving form has
exclusively been used to date:
where
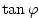 is evaluated at the is evaluated at the 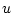 and and 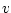 points
respectively. points
respectively.
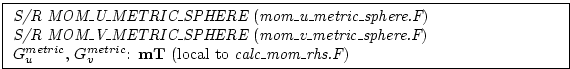



Next: 2.13.4 Non-hydrostatic metric terms
Up: 2.13 Flux-form momentum equations
Previous: 2.13.2 Coriolis terms
Contents
mitgcm-support@dev.mitgcm.org
| Copyright © 2002
Massachusetts Institute of Technology |
 |
|