| Symbol |
Description |
Units |
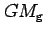 |
mass gravity constant of the geopotential model |
m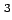 s s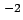 |
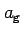 |
semi-major axis of the geopotential model |
meters |
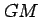 |
mass gravity constant of the reference ellipsoid |
m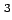 s s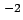 |
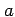 |
semi-major axis of the reference ellipsoid |
meters |
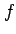 |
flattening parameter of the reference ellipsoid |
no units |
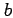 |
semi-minor axis of the reference ellipsoid |
meters |
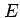 |
linear eccentricity |
meters |
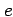 |
first (numerical) eccentricity |
no units |
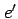 |
second (numerical) eccentricity |
no units |
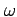 |
angular velocity of the Earth's rotation |
s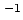 |
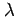 |
longitude |
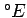 or radians or radians |
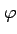 |
geographic latitude |
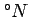 or radians or radians |
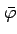 |
geocentric latitude |
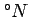 or radians or radians |
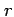 |
local elliptic radius |
meters |
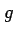 |
mean gravity |
ms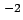 |
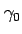 |
local normal gravity |
ms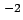 |
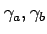 |
normal gravity at the
equator, at the poles |
ms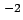 |
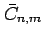 |
fully normalized
spherical harmonic coefficients |
no units |
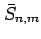 |
(or Stokes' coefficients) of the gravity model |
no units |
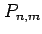 |
associated Legendre functions of the first kind |
no units |
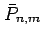 |
fully normalized harmonics |
no units |