First, let's write down formulas for quantities that we will
need lateron (Heiskanen and Moritz, 1967). First the relationship between Earth
flattening parameter ![]() , semi-major and semi-minor axes
, semi-major and semi-minor axes ![]() and
and ![]() :
:
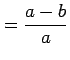 or or |
(1) | ||
| (2) | |||
| (linear eccentricity) | (3) | ||
| (first numerical eccentricity) | (4) | ||
| (second numerical eccentricity) | (5) | ||
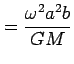 |
(an abbreviation) | (6) | |
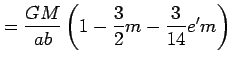 |
(gravity acc. at equator) | (7) | |
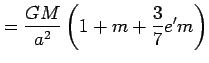 |
(gravity acc. at poles) | (8) | |
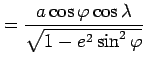 |
(Cartesian coordinates | (9) | |
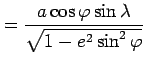 |
relative to center | (10) | |
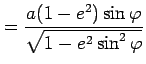 |
of Earth) | (11) |