


Next: 3.6 Reference ellipsoid
Up: 3 Geoid Height, Step
Previous: 3.4 Normal gravity
Contents
Make sure that your spherical harmonic coefficients are in the right
permanent tide system. Generally, satellite altimetry products use the
mean-tide system. Conversion between different permanent tide systems
involves either modifying one spherical harmonic coefficient or adding
a zonally uniform correction to the geoid undulations. To convert
zero-tide coefficients to mean-tide, use:
where 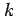 s the (fundamentally unknowable) zero frequency Love
number, which must be adopted. (For example, for EGM96,
s the (fundamentally unknowable) zero frequency Love
number, which must be adopted. (For example, for EGM96, 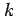 =0.3 was
adopted).
=0.3 was
adopted). 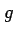 is the mean gravity.
is the mean gravity.
Alternatively, you could add the permanent tide correction in the
space domain, after computing the geoid height 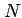 (Rapp, 1989):
(Rapp, 1989):
This latter method appears to be the preferred one, because you can
easily convert between permanent tide systems after the more expensive
computation of the geoid undulation.



Next: 3.6 Reference ellipsoid
Up: 3 Geoid Height, Step
Previous: 3.4 Normal gravity
Contents
mlosch@awi-bremerhaven.de
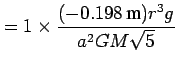
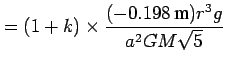
![]() (Rapp, 1989):
(Rapp, 1989):