



Next: 2.20.1 SHAP Diagnostics
Up: 2. Discretization and Algorithm
Previous: 2.19 Comparison of advection
Contents
2.20 Shapiro Filter
The Shapiro filter Shapiro [1970] is a high order horizontal
filter that efficiently remove small scale grid noise
without affecting the physical structures of a field.
It is applied at the end of the time step on both velocity and tracer fields.
Three different space operators are considered here (S1,S2 and S4).
They differs essentially by the sequence of derivative in
both X and Y directions. Consequently they show different
damping response function specially in the diagonal directions
X+Y and X-Y.
Space derivatives can be computed in the real space,
taken into account the grid spacing.
Alternatively, a pure computational filter can be defined,
using pure numerical differences and ignoring
grid spacing.
This later form is stable whatever the grid is, and therefore
specially useful for highly anisotropic grid such as spherical
coordinate grid.
A damping time-scale parameter
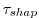 defines the strength of the filter damping.
defines the strength of the filter damping.
The 3 computational filter operators are :
In addition, the S2 operator can easily be extended to
a physical space filter:
with the Laplacian operator
 and a length scale parameter
and a length scale parameter 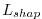 .
The stability of this S2g filter requires
.
The stability of this S2g filter requires
 .
.
Subsections




Next: 2.20.1 SHAP Diagnostics
Up: 2. Discretization and Algorithm
Previous: 2.19 Comparison of advection
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|







