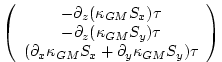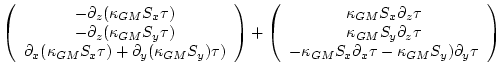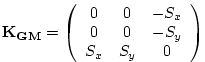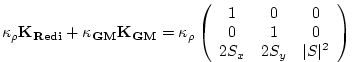Home Contact Us Site Map  
 
       
    next up previous contents
Next: 6.3.4 Variable Up: 6.3 Gent/McWiliams/Redi SGS Eddy Previous: 6.3.2 GM parameterization   Contents

6.3.3 Griffies Skew Flux

Griffies notes that the discretisation of bolus velocities involves multiple layers of differencing and interpolation that potentially lead to noisy fields and computational modes. He pointed out that the bolus flux can be re-written in terms of a non-divergent flux and a skew-flux:

$\displaystyle \bf {u}^* \tau$ $\displaystyle =$ $\displaystyle \left( \begin{array}{c} - \partial_z ( \kappa_{GM} S_x ) \tau \\ ... ...partial_x \kappa_{GM} S_x + \partial_y \kappa_{GM} S_y)\tau \end{array} \right)$  
  $\displaystyle =$ $\displaystyle \left( \begin{array}{c} - \partial_z ( \kappa_{GM} S_x \tau) \\ ... ...{GM} S_x \partial_x \tau - \kappa_{GM} S_y) \partial_y \tau \end{array} \right)$  

The first vector is non-divergent and thus has no effect on the tracer field and can be dropped. The remaining flux can be written:

$\displaystyle \bf {u}^* \tau = - \kappa_{GM} \bf {K}_{GM} \bf {\nabla} \tau$ (6.10)

where

$\displaystyle \bf {K}_{GM} = \left( \begin{array}{ccc} 0 & 0 & -S_x \\ 0 & 0 & -S_y \\ S_x & S_y & 0 \end{array} \right)$ (6.11)

is an anti-symmetric tensor.

This formulation of the GM parameterization involves fewer derivatives than the original and also involves only terms that already appear in the Redi mixing scheme. Indeed, a somewhat fortunate cancellation becomes apparent when we use the GM parameterization in conjunction with the Redi isoneutral mixing scheme:

$\displaystyle \kappa_\rho \bf {K}_{Redi} \bf {\nabla} \tau - u^* \tau = ( \kappa_\rho \bf {K}_{Redi} + \kappa_{GM} \bf {K}_{GM} ) \bf {\nabla} \tau$ (6.12)

In the instance that $ \kappa_{GM} = \kappa_{\rho}$ then

$\displaystyle \kappa_\rho \bf {K}_{Redi} + \kappa_{GM} \bf {K}_{GM} = \kappa_\r... ...c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 2 S_x & 2 S_y & \vert S\vert^2 \end{array} \right)$ (6.13)

which differs from the variable Laplacian diffusion tensor by only two non-zero elements in the $ z$-row.

\fbox{ \begin{minipage}{4.75in} {\em S/R GMREDI\_CALC\_TENSOR} ({\em pkg/gmredi/... ...ument on exit) \par $S_y$: {\bf SlopeY} (argument on exit) \par \end{minipage} }

next up previous contents
Next: 6.3.4 Variable Up: 6.3 Gent/McWiliams/Redi SGS Eddy Previous: 6.3.2 GM parameterization   Contents
mitgcm-support@dev.mitgcm.org
Copyright © 2002 Massachusetts Institute of Technology