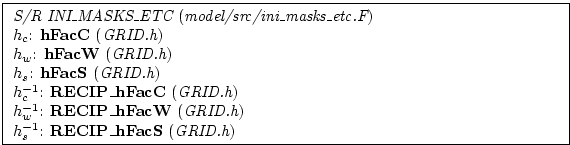Home Contact Us Site Map  
 
       
    next up previous contents
Next: 2.11 Continuity and horizontal Up: 2.10 Spatial discretization of Previous: 2.10.6 Vertical grid   Contents

2.10.7 Topography: partially filled cells

Figure 2.11: A schematic of the x-r plane showing the location of the non-dimensional fractions $ h_c$ and $ h_w$. The physical thickness of a tracer cell is given by $ h_c(i,j,k) \Delta r_f(k)$ and the physical thickness of the open side is given by $ h_w(i,j,k) \Delta r_f(k)$.
\resizebox{4.5in}{!}{\includegraphics{part2/vgrid-xz.eps}}

[5] presented two alternatives to the step-wise finite difference representation of topography. The method is known to the engineering community as intersecting boundary method. It involves allowing the boundary to intersect a grid of cells thereby modifying the shape of those cells intersected. We suggested allowing the topography to take on a piece-wise linear representation (shaved cells) or a simpler piecewise constant representation (partial step). Both show dramatic improvements in solution compared to the traditional full step representation, the piece-wise linear being the best. However, the storage requirements are excessive so the simpler piece-wise constant or partial-step method is all that is currently supported.

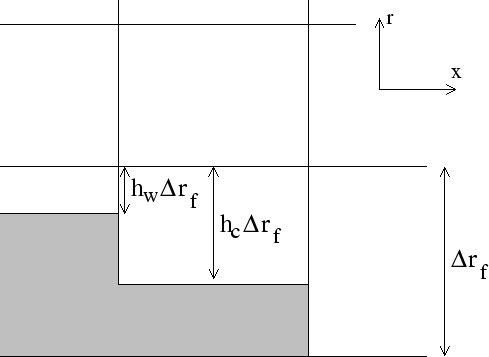
Fig. 2.11 shows a schematic of the x-r plane indicating how the thickness of a level is determined at tracer and u points. The physical thickness of a tracer cell is given by $ h_c(i,j,k) \Delta r_f(k)$ and the physical thickness of the open side is given by $ h_w(i,j,k) \Delta r_f(k)$. Three 3-D descriptors $ h_c$, $ h_w$ and $ h_s$ are used to describe the geometry: hFacC, hFacW and hFacS respectively. These are calculated in subroutine INI_MASKS_ETC along with there reciprocals RECIP_hFacC, RECIP_hFacW and RECIP_hFacS.

The non-dimensional fractions (or h-facs as we call them) are calculated from the model depth array and then processed to avoid tiny volumes. The rule is that if a fraction is less than hFacMin then it is rounded to the nearer of 0 or hFacMin or if the physical thickness is less than hFacMinDr then it is similarly rounded. The larger of the two methods is used when there is a conflict. By setting hFacMinDr equal to or larger than the thinnest nominal layers, $ \min{(\Delta z_f)}$, but setting hFacMin to some small fraction then the model will only lop thick layers but retain stability based on the thinnest unlopped thickness; $ \min{(\Delta z_f,\mbox{\bf hFacMinDr})}$.

\fbox{ \begin{minipage}{4.75in} {\em S/R INI\_MASKS\_ETC} ({\em model/src/ini\_m... ...RID.h}) \par $h_s^{-1}$: {\bf RECIP\_hFacS} ({\em GRID.h}) \par \end{minipage} }

next up previous contents
Next: 2.11 Continuity and horizontal Up: 2.10 Spatial discretization of Previous: 2.10.6 Vertical grid   Contents
mitgcm-support@dev.mitgcm.org
Copyright © 2002 Massachusetts Institute of Technology