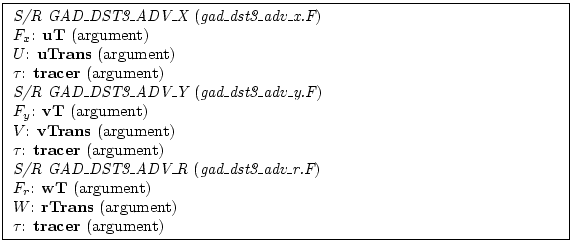|
 |
|||||||||||
 |
|
|||||||||||
 |
 |
|||||||||||
|
Next: 2.17.3 Third order direct Up: 2.17 Non-linear advection schemes Previous: 2.17.1 Second order flux Contents 2.17.2 Third order direct space time
The direct-space-time method deals with space and time discretization
together (other methods that treat space and time separately are known
collectively as the ``Method of Lines''). The Lax-Wendroff scheme
falls into this category; it adds sufficient diffusion to a second
order flux that the forward-in-time method is stable. The upwind
biased third order DST scheme is:
where
The coefficients
The DST3 method described above must be used in a forward-in-time
manner and is stable for
Next: 2.17.3 Third order direct Up: 2.17 Non-linear advection schemes Previous: 2.17.1 Second order flux Contents mitgcm-support@dev.mitgcm.org |
|||||||||||||||||||