Home Contact Us Site Map  
 
       
    next up previous contents
Next: 3.16.1 Configuration Up: 3. Getting Started with Previous: 3.15.6 Running the example   Contents


3.16 Gravity Plume On a Continental Slope

(in directory: verification/tutorial_plume_on_slope/)

Figure 3.16: Temperature after 23 hours of cooling. The cold dense water is mixed with ambient water as it accelerates down the slope and hence is warmed than the unmixed plume.
\includegraphics[width=\textwidth,height=.3\textheight]{s_examples/plume_on_slope/billows.eps}

An important test of any ocean model is the ability to represent the flow of dense fluid down a slope. One example of such a flow is a non-rotating gravity plume on a continental slope, forced by a limited area of surface cooling above a continental shelf. Because the flow is non-rotating, a two dimensional model can be used in the across slope direction. The experiment is non-hydrostatic and uses open-boundaries to radiate transients at the deep water end. (Dense flow down a slope can also be forced by a dense inflow prescribed on the continental shelf; this configuration is being implemented by the DOME (Dynamics of Overflow Mixing and Entrainment) collaboration to compare solutions in different models). The files for this experiment can be found in the verification directory under tutorial_plume_on_slope.

The fluid is initially unstratified. The surface buoyancy loss $ B_0$ (dimensions of L$ ^2$ T$ ^{-3}$ ) over a cross-shelf distance $ R$ causes vertical convective mixing and modifies the density of the fluid by an amount

$\displaystyle \Delta \rho = \frac{B_0 \rho_0 t}{g H}$ (3.82)

where $ H$ is the depth of the shelf, $ g$ is the acceleration due to gravity, $ t$ is time since onset of cooling and $ \rho_0$ is the reference density. Dense fluid slumps under gravity, with a flow speed close to the gravity wave speed:

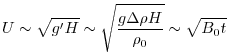$\displaystyle U \sim \sqrt{g' H} \sim \sqrt{ \frac{g \Delta \rho H}{\rho_0} } \sim \sqrt{B_0 t}$ (3.83)

A steady state is rapidly established in which the buoyancy flux out of the cooling region is balanced by the surface buoyancy loss. Then

$\displaystyle U \sim (B_0 R)^{1/3}$    ; $\displaystyle \Delta \rho \sim \frac{\rho_0}{g H} (B_0 R)^{2/3}$ (3.84)

The Froude number of the flow on the shelf is close to unity (but in practice slightly less than unity, giving subcritical flow). When the flow reaches the slope, it accelerates, so that it may become supercritical (provided the slope angle $ \alpha $ is steep enough). In this case, a hydraulic control is established at the shelf break. On the slope, where the Froude number is greater than one, and gradient Richardson number (defined as $ Ri \sim g' h^*/U^2$ where $ h^*$ is the thickness of the interface between dense and ambient fluid) is reduced below 1/4, Kelvin-Helmholtz instability is possible, and leads to entrainment of ambient fluid into the plume, modifying the density, and hence the acceleration down the slope. Kelvin-Helmholtz instability is suppressed at low Reynolds and Peclet numbers given by

$\displaystyle Re \sim \frac{U h}{ \nu} \sim \frac{(B_0 R)^{1/3} h}{\nu}$    ; $\displaystyle Pe = Re Pr$ (3.85)

where $ h$ is the depth of the dense fluid on the slope. Hence this experiment is carried out in the high Re, Pe regime. A further constraint is that the convective heat flux must be much greater than the diffusive heat flux (Nusselt number $ >> 1$ ). Then

$\displaystyle Nu = \frac{U h^* }{\kappa} >> 1$ (3.86)

Finally, since we have assumed that the convective mixing on the shelf occurs in a much shorter time than the horizontal equilibration, this implies $ H/R << 1$ .

Hence to summarize the important nondimensional parameters, and the limits we are considering:

$\displaystyle \frac{H}{R} << 1$    ; $\displaystyle Re >> 1$    ; $\displaystyle Pe >> 1$    ; $\displaystyle Nu >> 1$    ;     ; $\displaystyle Ri < 1/4$ (3.87)

In addition we are assuming that the slope is steep enough to provide sufficient acceleration to the gravity plume, but nonetheless much less that $ 1:1$ , since many Kelvin-Helmholtz billows appear on the slope, implying horizontal lengthscale of the slope $ >>$ the depth of the dense fluid.


Subsections
next up previous contents
Next: 3.16.1 Configuration Up: 3. Getting Started with Previous: 3.15.6 Running the example   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2011-01-09