|
|
|
|



Next: 3.16.5 Build and run
Up: 3.16 Gravity Plume On
Previous: 3.16.3 Code configuration
Contents
3.16.4 Model parameters
Table 3.2:
Model parameters used in the gravity plume experiment.
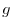
|
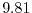 m s
m s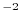
|
acceleration due to gravity |
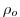
|
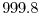 kg m
kg m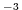
|
reference density |
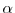
|
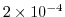 K
K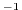
|
expansion coefficient |
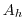
|
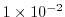 m
m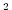 s
s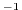
|
horizontal viscosity |
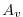
|
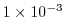 m
m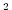 s
s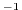
|
vertical viscosity |
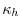
|
0
m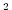 s
s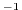
|
(explicit) horizontal diffusion |
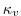
|
0
m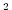 s
s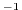
|
(explicit) vertical diffusion |
| |
|
|
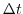
|
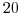 s
s |
time step |
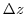
|
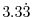 m
m |
vertical grid spacing |
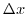
|
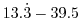 m
m |
horizontal grid spacing |
|
The model parameters (Table 3.2) are specified
in input/data and if not assume the default values defined in
model/src/set_defaults.F. A linear equation of state is used,
eosType='LINEAR', but only temperature is active, sBeta=0.E-4. For the given heat flux, 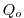 , the buoyancy forcing is
, the buoyancy forcing is
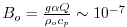 m
m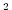 s
s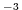 . Using
. Using 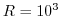 m, the shelf width, then this
gives a velocity scale of
m, the shelf width, then this
gives a velocity scale of
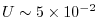 m s
m s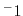 for the
initial front but will accelerate by an order of magnitude over the
slope. The temperature anomaly will be of order
for the
initial front but will accelerate by an order of magnitude over the
slope. The temperature anomaly will be of order
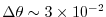 K. The viscosity is constant and gives a Reynolds
number of
K. The viscosity is constant and gives a Reynolds
number of 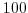 , using
, using 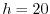 m for the initial front and will be an
order magnitude bigger over the slope. There is no explicit diffusion
but a non-linear advection scheme is used for temperature which adds
enough diffusion so as to keep the model stable. The time-step is set
to
m for the initial front and will be an
order magnitude bigger over the slope. There is no explicit diffusion
but a non-linear advection scheme is used for temperature which adds
enough diffusion so as to keep the model stable. The time-step is set
to 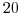 s and gives Courant number order one when the flow reaches the
bottom of the slope.
s and gives Courant number order one when the flow reaches the
bottom of the slope.



Next: 3.16.5 Build and run
Up: 3.16 Gravity Plume On
Previous: 3.16.3 Code configuration
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2011-01-09 |
 |
|







