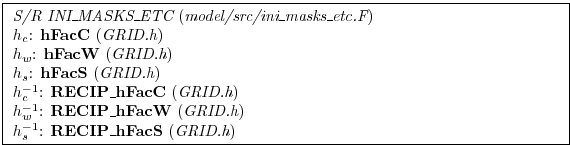2.11.6 Topography: partially filled cells

**Figure 2.12:** A schematic of the x-r plane showing the location of the non-dimensional fractions and . The physical thickness of a tracer cell is given by $h_c(i,j,k) \Delta r_f(k)$ and the physical thickness of the open side is given by $h_w(i,j,k) \Delta r_f(k)$ .
$\resizebox{4.5in}{!}{\includegraphics{s_algorithm/figs/vgrid-xz.eps}}$

Adcroft et al. [1997] presented two alternatives to the step-wise finite difference representation of topography. The method is known to the engineering community as intersecting boundary method. It involves allowing the boundary to intersect a grid of cells thereby modifying the shape of those cells intersected. We suggested allowing the topography to take on a piece-wise linear representation (shaved cells) or a simpler piecewise constant representation (partial step). Both show dramatic improvements in solution compared to the traditional full step representation, the piece-wise linear being the best. However, the storage requirements are excessive so the simpler piece-wise constant or partial-step method is all that is currently supported.

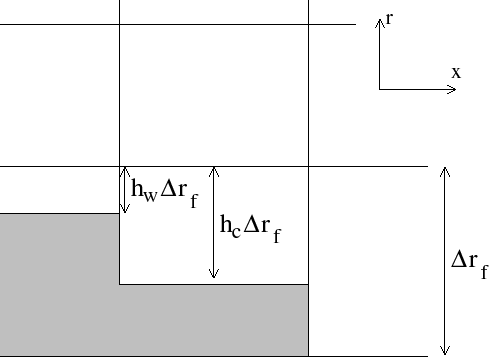
Fig. 2.12 shows a schematic of the x-r plane indicating how the thickness of a level is determined at tracer and u points. The physical thickness of a tracer cell is given by $h_c(i,j,k) \Delta r_f(k)$ and the physical thickness of the open side is given by $h_w(i,j,k) \Delta r_f(k)$ . Three 3-D descriptors

and

are used to describe the geometry: hFacC, hFacW and hFacS respectively. These are calculated in subroutine INI_MASKS_ETC along with there reciprocals RECIP_hFacC, RECIP_hFacW and RECIP_hFacS.

The non-dimensional fractions (or h-facs as we call them) are calculated from the model depth array and then processed to avoid tiny volumes. The rule is that if a fraction is less than hFacMin then it is rounded to the nearer of 0 or hFacMin or if the physical thickness is less than hFacMinDr then it is similarly rounded. The larger of the two methods is used when there is a conflict. By setting hFacMinDr equal to or larger than the thinnest nominal layers, $\min{(\Delta z_f)}$ , but setting hFacMin to some small fraction then the model will only lop thick layers but retain stability based on the thinnest unlopped thickness; $\min{(\Delta z_f,\mbox{\bf hFacMinDr})}$ .

$\fbox{ \begin{minipage}{4.75in} {\em S/R INI\_MASKS\_ETC} ({\em model/src/ini\_m... ...RID.h}) \par $h_s^{-1}$: {\bf RECIP\_hFacS} ({\em GRID.h}) \par \end{minipage} }$

Last update 2011-01-09