


Next: 4 Nota Bene
Up: 3 Geoid Height, Step
Previous: 3.7 Fully normalized associated
Contents
Now you are have all the quantities you need to compute the geoid
undulation 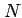 as a function of geographical longitude
as a function of geographical longitude 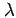 and
latitude
and
latitude 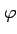 by the well-known formula (Heiskanen and Moritz, 1967)
by the well-known formula (Heiskanen and Moritz, 1967)
![\begin{displaymath}\begin{split}N(\lambda,\varphi) = \frac{GM_{\mathrm{g}}}{\gam...
...n(m\lambda)\right] \bar{P}_{nm}(\sin\bar{\varphi}). \end{split}\end{displaymath}](img117.png) |
(30) |
Here,
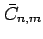 and
and
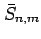 are the spherical harmonic
coefficients of degree
are the spherical harmonic
coefficients of degree 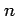 and order
and order 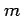 . Note that in this formula,
you need to use the mass gravity constant
. Note that in this formula,
you need to use the mass gravity constant
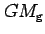 and the
scale factor
and the
scale factor
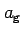 of the geopotential model.
of the geopotential model.
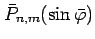 are the fully normalized harmonics,
or fully normalized associated Legendre functions. They are described
in the previous section (Section 3.7). Note that the
harmonics
are the fully normalized harmonics,
or fully normalized associated Legendre functions. They are described
in the previous section (Section 3.7). Note that the
harmonics
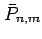 are evaluated at the geocentric latitude
are evaluated at the geocentric latitude
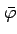 , and not at the geographical latitude
, and not at the geographical latitude
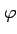 .
.
mlosch@awi-bremerhaven.de
![]() as a function of geographical longitude
as a function of geographical longitude ![]() and
latitude
and
latitude ![]() by the well-known formula (Heiskanen and Moritz, 1967)
by the well-known formula (Heiskanen and Moritz, 1967)