


Next: 3.8 Putting it all
Up: 3 Geoid Height, Step
Previous: 3.6 Reference ellipsoid
Contents
3.7 Fully normalized associated Legendre functions
For convenience, let us introduce the abbreviations
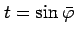 and
and
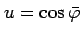 . The fully
normalized associated Legendre functions
. The fully
normalized associated Legendre functions
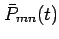 ,
sometimes also called fully normalized harmonics, can be computed from
the conventional associated Legendre functions
,
sometimes also called fully normalized harmonics, can be computed from
the conventional associated Legendre functions 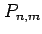 by
(Torge, 1991):
by
(Torge, 1991):
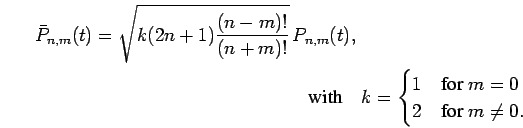 |
(25) |
The associated Legendre functions
can be computed with the following recursive formulas
(e.g., Bronstein and Semendjajew, 1991, Abramowitz and Stegun, 1972):
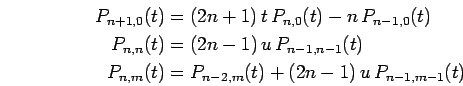 |
(26) |
with the starting values
However, these recursion formulas become numerically unstable for
large 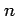 and
and 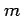 (
(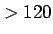 ) and you may have to use other, more
sophisticated formulas. These can be found in, for example,
Paul (1978) and Holmes and Featherstone (2002).
Here, we reproduce one method from
Holmes and Featherstone (2002) for convenience:
) and you may have to use other, more
sophisticated formulas. These can be found in, for example,
Paul (1978) and Holmes and Featherstone (2002).
Here, we reproduce one method from
Holmes and Featherstone (2002) for convenience:
For the fully normalized non-sectorial (i.e., 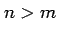 )
)
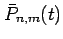 you can use the following recursion:
you can use the following recursion:
The sectorial (i.e. 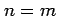 )
)
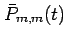 serve as
seed values for the recursion in (27). Starting from
serve as
seed values for the recursion in (27). Starting from
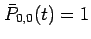 and
and
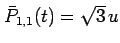 , they
can be computed from
, they
can be computed from



Next: 3.8 Putting it all
Up: 3 Geoid Height, Step
Previous: 3.6 Reference ellipsoid
Contents
mlosch@awi-bremerhaven.de
![]() and
and
![]() . The fully
normalized associated Legendre functions
. The fully
normalized associated Legendre functions
![]() ,
sometimes also called fully normalized harmonics, can be computed from
the conventional associated Legendre functions
,
sometimes also called fully normalized harmonics, can be computed from
the conventional associated Legendre functions ![]() by
(Torge, 1991):
by
(Torge, 1991):
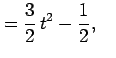
![]() )
)
![]() you can use the following recursion:
you can use the following recursion:
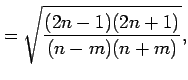
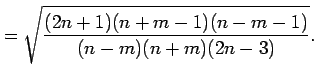
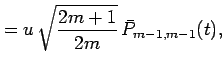 for all
for all 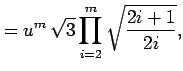 for all
for all