|
|
|
|



Next: 3.18.2 Implementation of the
Up: 3.18 Global Ocean State
Previous: 3.18 Global Ocean State
Contents
This experiment illustrates the optimization capacity of the MITgcm: here,
a high level description.
In this tutorial, a very simple case is used to illustrate the optimization
capacity of the MITgcm. Using an ocean configuration with realistic geography
and bathymetry on a
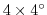 spherical polar grid, we estimate a
time-independent surface heat flux adjustment
spherical polar grid, we estimate a
time-independent surface heat flux adjustment
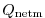 that attempts
to bring the model climatology into consistency with observations (Levitus
dataset, Levitus and T.P.Boyer [1994a]). The files for this experiment can be found in the
verification directory under tutorial_global_oce_optim.
that attempts
to bring the model climatology into consistency with observations (Levitus
dataset, Levitus and T.P.Boyer [1994a]). The files for this experiment can be found in the
verification directory under tutorial_global_oce_optim.
This adjustment
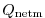 (a 2D field only function of longitude and
latitude) is the control variable of an optimization problem. It is inferred
by an iterative procedure using an `adjoint technique' and a least-squares
method (see, for example, Stammer et al. [002a] and Ferreira et al. [2005]).
(a 2D field only function of longitude and
latitude) is the control variable of an optimization problem. It is inferred
by an iterative procedure using an `adjoint technique' and a least-squares
method (see, for example, Stammer et al. [002a] and Ferreira et al. [2005]).
The ocean model is run forward in time and the quality of the solution is
determined by a cost function, 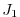 , a measure of the departure of the model
climatology from observations:
, a measure of the departure of the model
climatology from observations:
![$\displaystyle J_1=\frac{1}{N}\sum_{i=1}^N \left[ \frac{\overline{T}_i-\overline{T}_i^{lev}}{\sigma_i^T}\right]^2$](img1710.png) |
(3.91) |
where
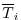 and
and
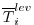 are, respectively, the model
and observed potential temperature at each
grid point
are, respectively, the model
and observed potential temperature at each
grid point 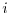 . The differences are weighted by an a priori uncertainty
. The differences are weighted by an a priori uncertainty
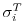 on observations (as provided by Levitus and T.P.Boyer [1994a]). The error
on observations (as provided by Levitus and T.P.Boyer [1994a]). The error
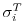 is only a function of depth and varies from 0.5 at the surface to
0.05 K at the bottom of the ocean, mainly reflecting the decreasing
temperature variance with depth (Fig. 3.21a). A value of
is only a function of depth and varies from 0.5 at the surface to
0.05 K at the bottom of the ocean, mainly reflecting the decreasing
temperature variance with depth (Fig. 3.21a). A value of 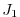 of
order 1 means that the model is, on average, within observational
uncertainties.
of
order 1 means that the model is, on average, within observational
uncertainties.
The cost function also places constraints on the adjustment to insure it is
"reasonable", i.e. of order of the uncertainties on the observed surface heat
flux:
![$\displaystyle J_2 = \frac{1}{N} \sum_{i=1}^N \left[\frac{Q_\mathrm{netm}}{\sigma^Q_i} \right]^2$](img1715.png) |
(3.92) |
where
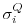 are the a priori errors on the observed heat flux as
estimated by Stammer et al. (2002) from 30% of local root-mean-square
variability of the NCEP forcing field (Fig 3.21b).
are the a priori errors on the observed heat flux as
estimated by Stammer et al. (2002) from 30% of local root-mean-square
variability of the NCEP forcing field (Fig 3.21b).
The total cost function is defined as
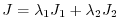 where
where
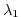 and
and 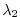 are weights controlling the relative contribution
of the two components. The adjoint model then yields the sensitivities
are weights controlling the relative contribution
of the two components. The adjoint model then yields the sensitivities
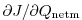 of
of 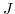 relative to the 2D fields
relative to the 2D fields
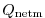 . Using a line-searching algorithm (Gilbert and Lemaréchal [1989]),
. Using a line-searching algorithm (Gilbert and Lemaréchal [1989]),
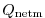 is adjusted then in the sense to
reduce
is adjusted then in the sense to
reduce  -- the procedure is repeated until convergence.
-- the procedure is repeated until convergence.
Fig. 3.22 shows the results of such an optimization. The
model is started from rest and from January-mean temperature and salinity
initial conditions taken from the Levitus dataset. The experiment is run a year
and the averaged temperature over the whole run (i.e. annual mean) is used
in the cost function (3.92) to evaluate the model3.1. Only the
top 2 levels are used. The first guess
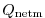 is chosen to be
zero. The weights
is chosen to be
zero. The weights 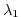 and
and 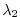 are set to 1 and 2, respectively.
The total cost function converges after 15 iterations, decreasing from 6.1 to
2.7 (the temperature contribution decreases from 6.1 to 1.8 while the heat
flux one increases from 0 to 0.42). The right panels of Fig. (3.22)
illustrate the evolution of the temperature error at the surface from
iteration 0 to iteration 15. Unsurprisingly, the largest errors at iteration 0
(up to 6
are set to 1 and 2, respectively.
The total cost function converges after 15 iterations, decreasing from 6.1 to
2.7 (the temperature contribution decreases from 6.1 to 1.8 while the heat
flux one increases from 0 to 0.42). The right panels of Fig. (3.22)
illustrate the evolution of the temperature error at the surface from
iteration 0 to iteration 15. Unsurprisingly, the largest errors at iteration 0
(up to 6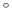 C, top left panels) are found in the Western boundary
currents. After optimization, the departure of the model temperature from
observations is reduced to 1
C, top left panels) are found in the Western boundary
currents. After optimization, the departure of the model temperature from
observations is reduced to 1 C or less almost everywhere except in the
Pacific Equatorial Cold Tongue. Comparison of the initial temperature
error (top, right) and heat flux adjustment (bottom, left) shows that the
system basically increased the heat flux out of the ocean where temperatures
were too warm and vice-versa. Obviously, heat flux uncertainties are not the
sole responsible for temperature errors and the heat flux adjustment partly
compensates the poor representation of narrow currents (Western boundary
currents, Equatorial currents) at
C or less almost everywhere except in the
Pacific Equatorial Cold Tongue. Comparison of the initial temperature
error (top, right) and heat flux adjustment (bottom, left) shows that the
system basically increased the heat flux out of the ocean where temperatures
were too warm and vice-versa. Obviously, heat flux uncertainties are not the
sole responsible for temperature errors and the heat flux adjustment partly
compensates the poor representation of narrow currents (Western boundary
currents, Equatorial currents) at
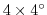 resolution. This is
allowed by the large a priori error on the heat flux (Fig. 3.21).
The Pacific Cold Tongue is a counter example: there, heat fluxes uncertainties
are fairly small (about 20 W.m
resolution. This is
allowed by the large a priori error on the heat flux (Fig. 3.21).
The Pacific Cold Tongue is a counter example: there, heat fluxes uncertainties
are fairly small (about 20 W.m ), and a large temperature errors
remains after optimization.
), and a large temperature errors
remains after optimization.
In the following, section 2 describes in details the implementation of the
control variable
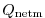 , the cost function
, the cost function 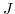 and the I/O required
for the communication between the model and the line-search. Instructions to
compile the MITgcm and its adjoint and the line-search algorithm are given in
section 3. The method used to run the experiment is described in section 4.
and the I/O required
for the communication between the model and the line-search. Instructions to
compile the MITgcm and its adjoint and the line-search algorithm are given in
section 3. The method used to run the experiment is described in section 4.
Figure 3.21:
A priori errors on potential temperature (left, in  C) and
surface heat flux (right, in W m
C) and
surface heat flux (right, in W m ) used to compute the cost
terms
) used to compute the cost
terms 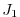 and
and 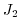 , respectively.
, respectively.
|
|
Figure 3.22:
Initial annual mean surface heat flux (top right in W.m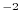 ) and
adjustment obtained at iteration 15 (bottom right). Averaged difference
between model and observed potential temperatures at the surface (in
) and
adjustment obtained at iteration 15 (bottom right). Averaged difference
between model and observed potential temperatures at the surface (in  C)
before optimization (iteration 0, top right) and after optimization
(iteration 15, bottom right). Contour intervals for heat flux and temperature
are 25 W.m
C)
before optimization (iteration 0, top right) and after optimization
(iteration 15, bottom right). Contour intervals for heat flux and temperature
are 25 W.m and 1
and 1 C, respectively. A positive flux is out of the
ocean.
C, respectively. A positive flux is out of the
ocean.
|
|



Next: 3.18.2 Implementation of the
Up: 3.18 Global Ocean State
Previous: 3.18 Global Ocean State
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|








![$\displaystyle J_1=\frac{1}{N}\sum_{i=1}^N \left[ \frac{\overline{T}_i-\overline{T}_i^{lev}}{\sigma_i^T}\right]^2$](img1710.png)
![$\displaystyle J_2 = \frac{1}{N} \sum_{i=1}^N \left[\frac{Q_\mathrm{netm}}{\sigma^Q_i} \right]^2$](img1715.png)
![\includegraphics[width=\textwidth,height=.3\textheight]{s_examples/global_oce_optim/Error.eps}](img1721.png)
![\includegraphics[width=\textwidth,height=.3\textheight]{s_examples/global_oce_optim/Tutorial_fig.eps}](img1722.png)


