|
|
|
|



Next: 1.3.6 Finding the pressure
Up: 1.3 Continuous equations in
Previous: 1.3.4 Hydrostatic, Quasi-hydrostatic, Quasi-nonhydrostatic
Contents
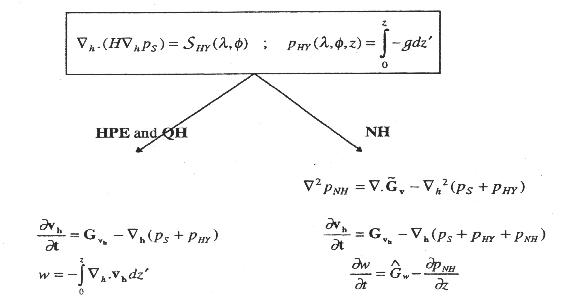
The method of solution employed in the HPE, QH and
NH models is summarized in Figure 1.17.
Under all dynamics, a 2-d elliptic equation is
first solved to find the surface pressure and the hydrostatic pressure at
any level computed from the weight of fluid above. Under HPE and
QH dynamics, the horizontal momentum equations are then stepped
forward and 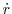 found from continuity. Under NH dynamics a
3-d elliptic equation must be solved for the non-hydrostatic pressure before
stepping forward the horizontal momentum equations;
found from continuity. Under NH dynamics a
3-d elliptic equation must be solved for the non-hydrostatic pressure before
stepping forward the horizontal momentum equations; 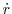 is found by
stepping forward the vertical momentum equation.
is found by
stepping forward the vertical momentum equation.
Figure 1.17:
Basic solution strategy in MITgcm. HPE and QH
forms diagnose the vertical velocity, in NH a prognostic
equation for the vertical velocity is integrated.
|
|
There is no penalty in implementing QH over HPE except, of
course, some complication that goes with the inclusion of
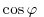 Coriolis terms and the relaxation of the shallow atmosphere approximation.
But this leads to negligible increase in computation. In NH, in
contrast, one additional elliptic equation - a three-dimensional one - must
be inverted for
Coriolis terms and the relaxation of the shallow atmosphere approximation.
But this leads to negligible increase in computation. In NH, in
contrast, one additional elliptic equation - a three-dimensional one - must
be inverted for 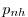 . However the `overhead' of the NH model is
essentially negligible in the hydrostatic limit (see detailed discussion in
Marshall et al, 1997) resulting in a non-hydrostatic algorithm that, in the
hydrostatic limit, is as computationally economic as the HPEs.
. However the `overhead' of the NH model is
essentially negligible in the hydrostatic limit (see detailed discussion in
Marshall et al, 1997) resulting in a non-hydrostatic algorithm that, in the
hydrostatic limit, is as computationally economic as the HPEs.



Next: 1.3.6 Finding the pressure
Up: 1.3 Continuous equations in
Previous: 1.3.4 Hydrostatic, Quasi-hydrostatic, Quasi-nonhydrostatic
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|