|
|
|
|



Next: 5.1.1 Forward or direct
Up: 5. Automatic Differentiation
Previous: 5. Automatic Differentiation
Contents
5.1 Some basic algebra
Let 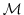 be a general nonlinear, model, i.e. a
mapping from the
be a general nonlinear, model, i.e. a
mapping from the 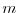 -dimensional space
-dimensional space
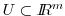 of input variables
of input variables
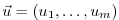 (model parameters, initial conditions, boundary conditions
such as forcing functions) to the
(model parameters, initial conditions, boundary conditions
such as forcing functions) to the 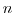 -dimensional space
-dimensional space
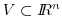 of
model output variable
of
model output variable
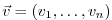 (model state, model diagnostics, objective function, ...)
under consideration,
(model state, model diagnostics, objective function, ...)
under consideration,
The vectors
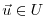 and
and 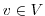 may be represented w.r.t.
some given basis vectors
may be represented w.r.t.
some given basis vectors
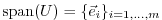 and
and
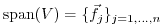 as
as
Two routes may be followed to determine the sensitivity of the
output variable 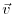 to its input
to its input 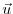 .
.
Subsections
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|







