Home Contact Us Site Map  
 
       
    next up previous contents
Next: 9.1.2 Time-extrapolation of tracer Up: 9.1 Other Time-stepping Options Previous: 9.1 Other Time-stepping Options   Contents

9.1.1 Adams-Bashforth III

Figure 9.1: Comparison of the oscillatory response of Adams-Bashforth scheme.
\resizebox{10cm}{!}{\includegraphics{s_under_dvlp/figs/stab_AB3_oscil.eps}}

The third-order Adams-Bashforth time stepping (AB-3) provides several advantages (see, e.g., Durran [1991]) compared to the default quasi-second order Adams-Bashforth (AB-2):

  • higher accuracy;
  • stable with a longer time-step;
  • no additional computation (just requires the storage of one additional time level).

The $ 3^{rd}$ order Adams-Bashforth can be used to extrapolate forward in time the tendency (replacing equation 2.24) which writes:

$\displaystyle G_\tau^{(n+1/2)} = ( 1 + \alpha_{AB} + \beta_{AB}) G_\tau^n - ( \alpha_{AB} + 2 \beta_{AB}) G_\tau^{n-1} + \beta_{AB} G_\tau^{n-2}$ (9.1)

The 3rd order AB is obtained with $ (\alpha_{AB},\,\beta_{AB}) = (1/2,\,5/12)$ . Note that selecting $ (\alpha_{AB},\,\beta_{AB}) = (1/2+\epsilon_{AB},\,0)$ one recovers the quasi-2nd order AB.

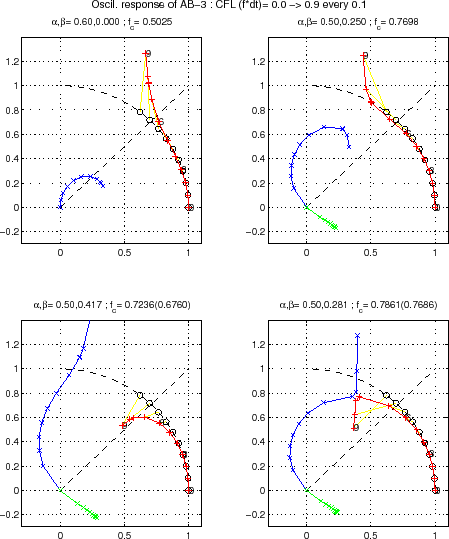
The AB-3 time stepping improves the stability limit for an oscillatory problem like advection or Coriolis. As seen from Fig.9.1, it remains stable up to a CFL of 0.72, compared to only 0.50 with AB-2 and $ \epsilon_{AB} = 0.1$ . It is interesting to note that the stability limit can be further extended up to a CFL of 0.786 for an oscillatory problem (see fig.9.1) using $ (\alpha_{AB},\,\beta_{AB}) = (0.5,\,0.2811)$ but then the scheme is only 2nd order accurate.

Figure 9.2: Comparison of the damping (diffusion like) response of Adams-Bashforth schemes.
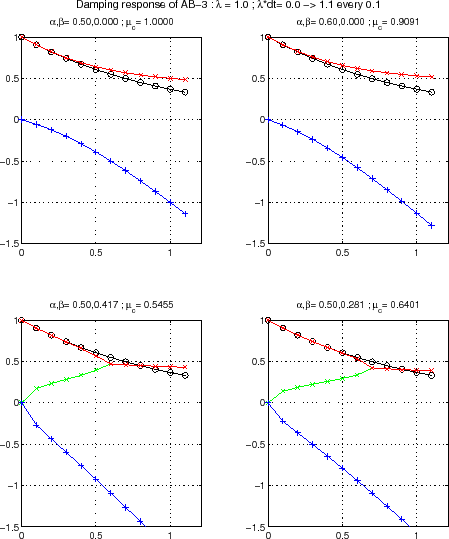
\resizebox{10cm}{!}{\includegraphics{s_under_dvlp/figs/stab_AB3_dampR.eps}}

However, the behavior of the AB-3 for a damping problem (like diffusion) is less favorable, since the stability limit is reduced to 0.54 only (and 0.64 with $ \beta_{AB} = 0.2811$ ) compared to 1. (and 0.9 with $ \epsilon_{AB} = 0.1$ ) with the AB-2 (see fig.9.2).

A way to enable the use of a longer time step is to keep the dissipation terms outside the AB extrapolation (setting momDissip_In_AB=.FALSE. in main parameter file "data", namelist PARM03), thus returning to a simple forward time-stepping for dissipation, and to use AB-3 only for advection and Coriolis terms.

The AB-3 time stepping is activated by defining the option #define ALLOW_ADAMSBASHFORTH_3 in "CPP_OPTIONS.h". The parameters $ \alpha_{AB},\beta_{AB}$ can be set from the main parameter file "data" (namelist PARM03) and their default value corresponds to the 3rd order Adams-Bashforth. A simple example is provided in "verification/advect_xy/input.ab3_c4".

The AB-3 is not yet available for the vertical momentum equation (Non-Hydrostatic) neither for passive tracers.

next up previous contents
Next: 9.1.2 Time-extrapolation of tracer Up: 9.1 Other Time-stepping Options Previous: 9.1 Other Time-stepping Options   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2018-01-23