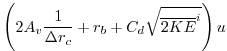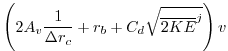Home Contact Us Site Map  
 
       
    next up previous contents
Next: 2.14.7 Derivation of discrete Up: 2.14 Flux-form momentum equations Previous: 2.14.5 Lateral dissipation   Contents

2.14.6 Vertical dissipation

Vertical viscosity terms are discretized with only partial adherence to the variable grid lengths introduced by the finite volume formulation. This reduces the formal accuracy of these terms to just first order but only next to boundaries; exactly where other terms appear such as linear and quadratic bottom drag.

$\displaystyle G_u^{v-diss}$ $\displaystyle =$ $\displaystyle \frac{1}{\Delta r_f h_w} \delta_k \tau_{13}$ (2.132)
$\displaystyle G_v^{v-diss}$ $\displaystyle =$ $\displaystyle \frac{1}{\Delta r_f h_s} \delta_k \tau_{23}$ (2.133)
$\displaystyle G_w^{v-diss}$ $\displaystyle =$ $\displaystyle \epsilon_{nh} \frac{1}{\Delta r_f h_d} \delta_k \tau_{33}$ (2.134)

represents the general discrete form of the vertical dissipation terms.

In the interior the vertical stresses are discretized:

$\displaystyle \tau_{13}$ $\displaystyle =$ $\displaystyle A_v \frac{1}{\Delta r_c} \delta_k u$ (2.135)
$\displaystyle \tau_{23}$ $\displaystyle =$ $\displaystyle A_v \frac{1}{\Delta r_c} \delta_k v$ (2.136)
$\displaystyle \tau_{33}$ $\displaystyle =$ $\displaystyle A_v \frac{1}{\Delta r_f} \delta_k w$ (2.137)

It should be noted that in the non-hydrostatic form, the stress tensor is even less consistent than for the hydrostatic (see Wajsowicz [1993]). It is well known how to do this properly (see Griffies and Hallberg [2000]) and is on the list of to-do's.

\fbox{ \begin{minipage}{4.75in} {\em S/R MOM\_U\_RVISCLFUX} ({\em mom\_u\_rviscf... ...}) \par $\tau_{23}$: {\bf vrf} (local to {\em mom\_fluxform.F}) \end{minipage} }

As for the lateral viscous terms, the free-slip condition is equivalent to simply setting the stress to zero on boundaries. The no-slip condition is implemented as an additional term acting on top of the interior and free-slip stresses. Bottom drag represents additional friction, in addition to that imposed by the no-slip condition at the bottom. The drag is cast as a stress expressed as a linear or quadratic function of the mean flow in the layer above the topography:

$\displaystyle \tau_{13}^{bottom-drag}$ $\displaystyle =$ $\displaystyle \left( 2 A_v \frac{1}{\Delta r_c} + r_b + C_d \sqrt{ \overline{2 KE}^i } \right) u$ (2.138)
$\displaystyle \tau_{23}^{bottom-drag}$ $\displaystyle =$ $\displaystyle \left( 2 A_v \frac{1}{\Delta r_c} + r_b + C_d \sqrt{ \overline{2 KE}^j } \right) v$ (2.139)

where these terms are only evaluated immediately above topography. $ r_b$ (bottomDragLinear) has units of $ m s^{-1}$ and a typical value of the order 0.0002 $ m s^{-1}$ . $ C_d$ (bottomDragQuadratic) is dimensionless with typical values in the range 0.001-0.003.

\fbox{ \begin{minipage}{4.75in} {\em S/R MOM\_U\_BOTTOMDRAG} ({\em mom\_u\_botto... ...m-drag}/\Delta r_f$: {\bf vf} (local to {\em mom\_fluxform.F}) \end{minipage} }

next up previous contents
Next: 2.14.7 Derivation of discrete Up: 2.14 Flux-form momentum equations Previous: 2.14.5 Lateral dissipation   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2018-01-23