Home Contact Us Site Map  
 
       
    next up previous contents
Next: 2.15.5 Gradient of Bernoulli Up: 2.15 Vector invariant momentum Previous: 2.15.3 Coriolis terms   Contents

2.15.4 Shear terms

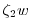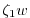The shear terms ($ \zeta_2w$ and $ \zeta_1w$ ) are are discretized to guarantee that no spurious generation of kinetic energy is possible; the horizontal gradient of Bernoulli function has to be consistent with the vertical advection of shear:

$\displaystyle G_u^{\zeta_2 w}$ $\displaystyle =$ $\displaystyle \frac{1}{ {\cal A}_w \Delta r_f h_w } \overline{ \overline{ {\cal A}_c w }^i ( \delta_k u - \epsilon_{nh} \delta_j w ) }^k$ (2.153)
$\displaystyle G_v^{\zeta_1 w}$ $\displaystyle =$ $\displaystyle \frac{1}{ {\cal A}_s \Delta r_f h_s } \overline{ \overline{ {\cal A}_c w }^i ( \delta_k u - \epsilon_{nh} \delta_j w ) }^k$ (2.154)

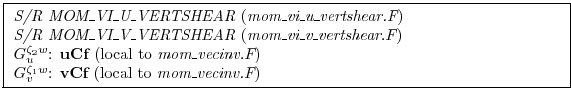
\fbox{ \begin{minipage}{4.75in} {\em S/R MOM\_VI\_U\_VERTSHEAR} ({\em mom\_vi\_u... ...par $G_v^{\zeta_1 w}$: {\bf vCf} (local to {\em mom\_vecinv.F}) \end{minipage} }


mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2018-01-23