Home Contact Us Site Map  
 
       
    next up previous contents
Next: 2.17 Linear advection schemes Up: 2.16 Tracer equations Previous: 2.16 Tracer equations   Contents


2.16.1 Time-stepping of tracers: ABII

The default advection scheme is the centered second order method which requires a second order or quasi-second order time-stepping scheme to be stable. Historically this has been the quasi-second order Adams-Bashforth method (ABII) and applied to all terms. For an arbitrary tracer, $ \tau$ , the forced advection-diffusion equation reads:

$\displaystyle \partial_t \tau + G_{adv}^\tau = G_{diff}^\tau + G_{forc}^\tau$ (2.166)

where $ G_{adv}^\tau$ , $ G_{diff}^\tau$ and $ G_{forc}^\tau$ are the tendencies due to advection, diffusion and forcing, respectively, namely:
$\displaystyle G_{adv}^\tau$ $\displaystyle =$ $\displaystyle \partial_x u \tau + \partial_y v \tau + \partial_r w \tau - \tau \nabla \cdot {\bf v}$ (2.167)
$\displaystyle G_{diff}^\tau$ $\displaystyle =$ $\displaystyle \nabla \cdot {\bf K} \nabla \tau$ (2.168)

and the forcing can be some arbitrary function of state, time and space.

The term, $ \tau \nabla \cdot {\bf v}$ , is required to retain local conservation in conjunction with the linear implicit free-surface. It only affects the surface layer since the flow is non-divergent everywhere else. This term is therefore referred to as the surface correction term. Global conservation is not possible using the flux-form (as here) and a linearized free-surface (Campin et al. [2004]; Griffies and Hallberg [2000]).

The continuity equation can be recovered by setting $ G_{diff}=G_{forc}=0$ and $ \tau=1$ .

The driver routine that calls the routines to calculate tendencies are S/R CALC_GT and S/R CALC_GS for temperature and salt (moisture), respectively. These in turn call a generic advection diffusion routine S/R GAD_CALC_RHS that is called with the flow field and relevant tracer as arguments and returns the collective tendency due to advection and diffusion. Forcing is add subsequently in S/R CALC_GT or S/R CALC_GS to the same tendency array.

\fbox{ \begin{minipage}{4.75in} {\em S/R GAD\_CALC\_RHS} ({\em pkg/generic\_advd... ...\bf gTracer} (argument) \par $F_r$: {\bf fVerT} (argument) \par \end{minipage} }

The space and time discretization are treated separately (method of lines). Tendencies are calculated at time levels $ n$ and $ n-1$ and extrapolated to $ n+1/2$ using the Adams-Bashforth method:

$\displaystyle G^{(n+1/2)} = (\frac{3}{2} + \epsilon) G^{(n)} - (\frac{1}{2} + \epsilon) G^{(n-1)}$ (2.169)

where $ G^{(n)} = G_{adv}^\tau + G_{diff}^\tau + G_{src}^\tau$ at time step $ n$ . The tendency at $ n-1$ is not re-calculated but rather the tendency at $ n$ is stored in a global array for later re-use.

\fbox{ \begin{minipage}{4.75in} {\em S/R ADAMS\_BASHFORTH2} ({\em model/src/adam... ...gTrNm1} (argument) \par $\epsilon$: {\bf ABeps} (PARAMS.h) \par \end{minipage} }

The tracers are stepped forward in time using the extrapolated tendency:

$\displaystyle \tau^{(n+1)} = \tau^{(n)} + \Delta t G^{(n+1/2)}$ (2.170)

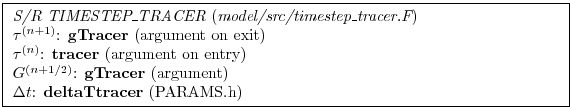
\fbox{ \begin{minipage}{4.75in} {\em S/R TIMESTEP\_TRACER} ({\em model/src/times... ... (argument) \par $\Delta t$: {\bf deltaTtracer} (PARAMS.h) \par \end{minipage} }

Strictly speaking the ABII scheme should be applied only to the advection terms. However, this scheme is only used in conjunction with the standard second, third and fourth order advection schemes. Selection of any other advection scheme disables Adams-Bashforth for tracers so that explicit diffusion and forcing use the forward method.

next up previous contents
Next: 2.17 Linear advection schemes Up: 2.16 Tracer equations Previous: 2.16 Tracer equations   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2018-01-23