2.19 Comparison of advection schemes

Table 2.2: Summary of the different advection schemes available in MITgcm. ``A.B.'' stands for Adams-Bashforth and ``DST'' for direct space time. The code corresponds to the number used to select the corresponding advection scheme in the parameter file (e.g., tempAdvScheme=3 in file data selects the 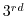$3^{rd}$ order upwind advection scheme for temperature).

Advection Scheme	code	use	use Multi-	Stencil	comments
		A.B.	dimension	(1 dim)
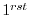$1^{rst}$ order upwind	1	No	Yes	3 pts	linear/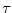 $\tau$ , non-linear/v
centered 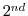$2^{nd}$ order	2	Yes	No	3 pts	linear
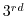$3^{rd}$ order upwind	3	Yes	No	5 pts	linear/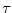 $\tau$
centered 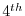$4^{th}$ order	4	Yes	No	5 pts	linear
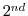$2^{nd}$ order DST (Lax-Wendroff)	20	No	Yes	3 pts	linear/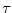 $\tau$ , non-linear/v
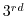$3^{rd}$ order DST	30	No	Yes	5 pts	linear/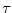 $\tau$ , non-linear/v
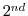$2^{nd}$ order-moment Prather	80	No	Yes
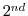$2^{nd}$ order Flux Limiters	77	No	Yes	5 pts	non-linear
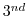$3^{nd}$ order DST Flux limiter	33	No	Yes	5 pts	non-linear
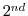$2^{nd}$ order-moment Prather w. limiter	81	No	Yes
piecewise parabolic w. ``null'' limiter	40	No	Yes
piecewise parabolic w. ``mono'' limiter	41	No	Yes
piecewise quartic w. ``null'' limiter	50	No	Yes
piecewise quartic w. ``mono'' limiter	51	No	Yes
piecewise quartic w. ``weno'' limiter	52	No	Yes
$7^{nd}$ order one-step method	7	No	Yes
with Monotonicity Preserving Limiter

Figs. 2.15, 2.16 and 2.17 show solutions to a simple diagonal advection problem using a selection of schemes for low, moderate and high Courant numbers, respectively. The top row shows the linear schemes, integrated with the Adams-Bashforth method. Theses schemes are clearly unstable for the high Courant number and weakly unstable for the moderate Courant number. The presence of false extrema is very apparent for all Courant numbers. The middle row shows solutions obtained with the unlimited but multi-dimensional schemes. These solutions also exhibit false extrema though the pattern now shows symmetry due to the multi-dimensional scheme. Also, the schemes are stable at high Courant number where the linear schemes weren't. The bottom row (left and middle) shows the limited schemes and most obvious is the absence of false extrema. The accuracy and stability of the unlimited non-linear schemes is retained at high Courant number but at low Courant number the tendency is to loose amplitude in sharp peaks due to diffusion. The one dimensional tests shown in Figs. 2.13 and 2.14 showed this phenomenon.

Finally, the bottom left and right panels use the same advection scheme but the right does not use the multi-dimensional method. At low Courant number this appears to not matter but for moderate Courant number severe distortion of the feature is apparent. Moreover, the stability of the multi-dimensional scheme is determined by the maximum Courant number applied of each dimension while the stability of the method of lines is determined by the sum. Hence, in the high Courant number plot, the scheme is unstable.

With many advection schemes implemented in the code two questions arise: ``Which scheme is best?'' and ``Why don't you just offer the best advection scheme?''. Unfortunately, no one advection scheme is ``the best'' for all particular applications and for new applications it is often a matter of trial to determine which is most suitable. Here are some guidelines but these are not the rule;