|
|
|
|



Next: 3. Getting Started with
Up: 2.21 Nonlinear Viscosities for
Previous: 2.21.1 Eddy Viscosity
Contents
The rotating, incompressible, Boussinesq equations of motion
Gill [1982] on a sphere can be written in Mercator projection
about a latitude 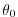 and geopotential height
and geopotential height 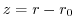 . The
nondimensional form of these equations is:
. The
nondimensional form of these equations is:
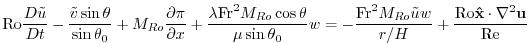 |
(2.225) |
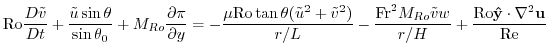 |
(2.226) |
Where
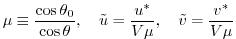 |
(2.229) |
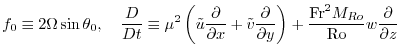 |
(2.230) |
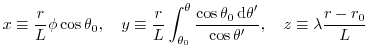 |
(2.231) |
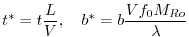 |
(2.232) |
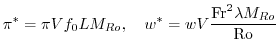 |
(2.233) |
![$\displaystyle {\rm Ro}\equiv\frac{V}{f_0 L},\ \ \ {M_{Ro}}\equiv \max[1,{\rm Ro}]$](img1095.png) |
(2.234) |
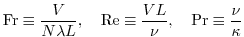 |
(2.235) |
Dimensional variables are denoted by an asterisk where necessary. If
we filter over a grid scale typical for ocean models (
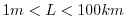 ,
,
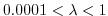 ,
,
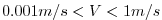 ,
,
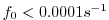 ,
,
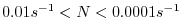 ), these equations are very well approximated
by
), these equations are very well approximated
by
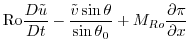 |
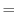 |
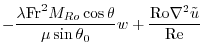 |
(2.236) |
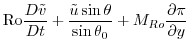 |
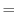 |
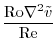 |
(2.237) |
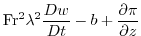 |
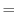 |
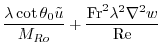 |
(2.238) |
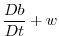 |
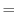 |
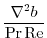 |
(2.239) |
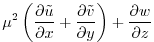 |
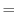 |
0 |
(2.240) |
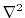 |
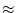 |
 |
(2.241) |
Neglecting the non-frictional terms on the right-hand side is usually
called the 'traditional' approximation. It is appropriate, with
either large aspect ratio or far from the tropics. This approximation
is used here, as it does not affect the form of the eddy stresses
which is the main topic. The frictional terms are preserved in this
approximate form for later comparison with eddy stresses.



Next: 3. Getting Started with
Up: 2.21 Nonlinear Viscosities for
Previous: 2.21.1 Eddy Viscosity
Contents
mitgcm-support@mitgcm.org
| Copyright © 2006
Massachusetts Institute of Technology |
Last update 2018-01-23 |
 |
|