


Next: 3.12.2 Discrete Numerical Configuration
Up: 3.12 Held-Suarez Atmosphere MITgcm
Previous: 3.12 Held-Suarez Atmosphere MITgcm
Contents
3.12.1 Overview
This example demonstrates using the MITgcm to simulate
the planetary atmospheric circulation in two ways.
In both cases the simulation is configured with flat orography.
In the first case shown a
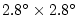 spherical polar
horizontal grid is employed. In the second case a cube-sphere horizontal
grid is used that projects a cube with face size of spherical polar
horizontal grid is employed. In the second case a cube-sphere horizontal
grid is used that projects a cube with face size of
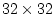 onto a
sphere.
Five pressure corrdinate levels are used in the vertical, ranging in thickness
from onto a
sphere.
Five pressure corrdinate levels are used in the vertical, ranging in thickness
from
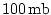 at the bottom of the atmosphere to at the bottom of the atmosphere to
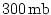 in the middle atmosphere.
The total depth of the atmosphere is in the middle atmosphere.
The total depth of the atmosphere is
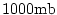 .
At this resolution, the configuration can be integrated forward for many years on a
single processor desktop computer. .
At this resolution, the configuration can be integrated forward for many years on a
single processor desktop computer.
The model is forced by relaxation to a radiative equilibrium profile
from Held and Suarez [26]. Initial conditions are a
statically stable thermal gradient and no motion. The atmosphere
in these experiments is dry and the only active ``physics'' are the
terms in the Held and Suarez [26] formula. The
MITgcm intermediate atmospheric physics package (see 6.10) and
MITgcm high-end physics package ( see ![[*]](crossref.png) ) are turned off.
Altogether, this yields the following forcing
(from Held and Suarez [26]) that is applied to the fluid: ) are turned off.
Altogether, this yields the following forcing
(from Held and Suarez [26]) that is applied to the fluid:
where
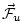 , ,
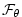 ,
are the forcing terms in the zonal and meridional
momentum and in the potential temperature
equations respectively.
The term ,
are the forcing terms in the zonal and meridional
momentum and in the potential temperature
equations respectively.
The term 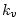 in equation (3.62) applies a
linear frictional drag (Rayleigh damping) that is active within the
planetary boundary layer. It is defined so as to decay with
height according to in equation (3.62) applies a
linear frictional drag (Rayleigh damping) that is active within the
planetary boundary layer. It is defined so as to decay with
height according to
where
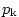 is the pressure level of the cell center for level is the pressure level of the cell center for level 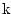 and
and 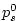 is the pressure at the base of the atmospheric column. is the pressure at the base of the atmospheric column.



Next: 3.12.2 Discrete Numerical Configuration
Up: 3.12 Held-Suarez Atmosphere MITgcm
Previous: 3.12 Held-Suarez Atmosphere MITgcm
Contents
mitgcm-support@dev.mitgcm.org
| Copyright © 2002
Massachusetts Institute of Technology |
 |
|







