


Next: 3.13.3 Discrete numerical configuration
Up: 3.13 Surface Driven Convection
Previous: 3.13.1 Overview
Contents
3.13.2 Equations solved
The model is configured in nonhydrostatic form, that is, all terms in the Navier
Stokes equations are retained and the pressure field is found, subject to appropriate
bounday condintions, through inversion of a three-dimensional elliptic equation.
The implicit free surface form of the
pressure equation described in Marshall et. al [39] is
employed. A horizontal Laplacian operator
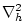 provides viscous
dissipation. The thermodynamic forcing appears as a sink in the potential temperature, provides viscous
dissipation. The thermodynamic forcing appears as a sink in the potential temperature,
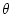 , equation ( , equation (![[*]](crossref.png) ). This produces a set of equations
solved in this configuration as follows: ). This produces a set of equations
solved in this configuration as follows:
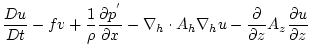 |
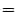 |
 |
(3.85) |
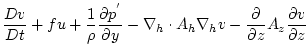 |
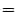 |
 |
(3.86) |
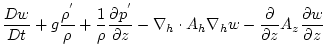 |
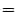 |
 |
(3.87) |
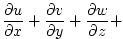 |
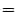 |
0 |
(3.88) |
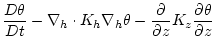 |
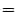 |
 |
(3.89) |
where
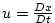 , ,
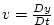 and and
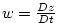 are the components of the
flow vector in directions are the components of the
flow vector in directions 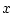 , , 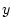 and and 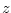 .
The pressure is diagnosed through inversion (subject to appropriate boundary
conditions) of a 3-D elliptic equation derived from the divergence of the momentum
equations and continuity (see section 1.3.6). .
The pressure is diagnosed through inversion (subject to appropriate boundary
conditions) of a 3-D elliptic equation derived from the divergence of the momentum
equations and continuity (see section 1.3.6).



Next: 3.13.3 Discrete numerical configuration
Up: 3.13 Surface Driven Convection
Previous: 3.13.1 Overview
Contents
mitgcm-support@dev.mitgcm.org
| Copyright © 2002
Massachusetts Institute of Technology |
 |
|







