Home Contact Us Site Map  
 
       
    next up previous contents
Next: 2.9.2 Non-linear free-surface Up: 2.9 Variants on the Previous: 2.9 Variants on the   Contents


2.9.1 Crank-Nickelson barotropic time stepping

The full implicit time stepping described previously is unconditionally stable but damps the fast gravity waves, resulting in a loss of potential energy. The modification presented now allows one to combine an implicit part ( $ \beta,\gamma$) and an explicit part ( $ 1-\beta,1-\gamma$) for the surface pressure gradient ($ \beta$) and for the barotropic flow divergence ($ \gamma$).
For instance, $ \beta=\gamma=1$ is the previous fully implicit scheme; $ \beta=\gamma=1/2$ is the non damping (energy conserving), unconditionally stable, Crank-Nickelson scheme; $ (\beta,\gamma)=(1,0)$ or $ =(0,1)$ corresponds to the forward - backward scheme that conserves energy but is only stable for small time steps.
In the code, $ \beta,\gamma$ are defined as parameters, respectively implicSurfPress, implicDiv2DFlow. They are read from the main parameter file "data" and are set by default to 1,1.

Equations 2.17 - 2.22 are modified as follows:

$\displaystyle \frac{ \vec{\bf v}^{n+1} }{ \Delta t } + {\bf\nabla}_h b_s [ \bet... ...ilon_{nh} {\bf\nabla}_h {\phi'_{nh}}^{n+1} = \frac{ \vec{\bf v}^* }{ \Delta t }$      


$\displaystyle \epsilon_{fs} \frac{ {\eta}^{n+1} - {\eta}^{n} }{ \Delta t} + {\b... ...\gamma \vec{\bf v}^{n+1} + (1-\gamma) \vec{\bf v}^{n}] dr = \epsilon_{fw} (P-E)$     (2.76)

where:
$\displaystyle \vec{\bf v}^*$ $\displaystyle =$ $\displaystyle \vec{\bf v} ^{n} + \Delta t \vec{\bf G}_{\vec{\bf v}} ^{(n+1/2)} ... ...t {\bf\nabla}_h b_s {\eta}^{n} + \Delta t {\bf\nabla}_h {\phi'_{hyd}}^{(n+1/2)}$  
$\displaystyle {\eta}^*$ $\displaystyle =$ $\displaystyle \epsilon_{fs} {\eta}^{n} + \epsilon_{fw} \Delta t (P-E) - \Delta ... ... \int_{R_{fixed}}^{R_o} [ \gamma \vec{\bf v}^* + (1-\gamma) \vec{\bf v}^{n}] dr$  


In the hydrostatic case ( $ \epsilon _{nh}=0$), allowing us to find $ {\eta}^{n+1}$, thus:

$\displaystyle \epsilon_{fs} {\eta}^{n+1} - {\bf\nabla}_h \cdot \beta\gamma \Delta t^2 b_s (R_o - R_{fixed}) {\bf\nabla}_h {\eta}^{n+1} = {\eta}^* $

and then to compute (CORRECTION_STEP):

$\displaystyle \vec{\bf v}^{n+1} = \vec{\bf v}^{*} - \beta \Delta t {\bf\nabla}_h b_s {\eta}^{n+1} $

Notes:

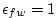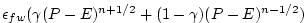
  1. The RHS term of equation 2.78 corresponds the contribution of fresh water flux (P-E) to the free-surface variations ( $ \epsilon_{fw}=1$, useRealFreshWater=TRUE in parameter file data). In order to remain consistent with the tracer equation, specially in the non-linear free-surface formulation, this term is also affected by the Crank-Nickelson time stepping. The RHS reads: $ \epsilon_{fw} ( \gamma (P-E)^{n+1/2} + (1-\gamma) (P-E)^{n-1/2} )$
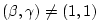  2. The non-hydrostatic part of the code has not yet been updated, and therefore cannot be used with $ (\beta,\gamma) \neq (1,1)$.
  3. The stability criteria with Crank-Nickelson time stepping for the pure linear gravity wave problem in cartesian coordinates is:
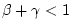    • $ \beta + \gamma < 1$ : unstable
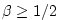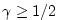    • $ \beta \geq 1/2$ and $ \gamma \geq 1/2$ : stable
    • $ \beta + \gamma \geq 1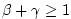$ : stable if

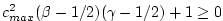      $\displaystyle c_{max}^2 (\beta - 1/2)(\gamma - 1/2) + 1 \geq 0 $

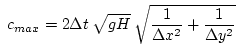
         with $\displaystyle ~ c_{max} = 2 \Delta t \: \sqrt{g H} \: \sqrt{ \frac{1}{\Delta x^2} + \frac{1}{\Delta y^2} } $

next up previous contents
Next: 2.9.2 Non-linear free-surface Up: 2.9 Variants on the Previous: 2.9 Variants on the   Contents
mitgcm-support@dev.mitgcm.org
Copyright © 2002 Massachusetts Institute of Technology