Home Contact Us Site Map  
 
       
    next up previous contents
Next: 6.4.2 KPP: Nonlocal K-Profile Up: 6.4 Ocean Packages Previous: 6.4 Ocean Packages   Contents

Subsections


6.4.1 GMREDI: Gent-McWilliams/Redi SGS Eddy Parameterization

There are two parts to the Redi/GM parameterization of geostrophic eddies. The first, the Redi scheme [Redi, 1982], aims to mix tracer properties along isentropes (neutral surfaces) by means of a diffusion operator oriented along the local isentropic surface. The second part, GM [Gent and McWilliams, 1990; Gent et al., 1995], adiabatically re-arranges tracers through an advective flux where the advecting flow is a function of slope of the isentropic surfaces.

The first GCM implementation of the Redi scheme was by Cox [1987] in the GFDL ocean circulation model. The original approach failed to distinguish between isopycnals and surfaces of locally referenced potential density (now called neutral surfaces) which are proper isentropes for the ocean. As will be discussed later, it also appears that the Cox implementation is susceptible to a computational mode. Due to this mode, the Cox scheme requires a background lateral diffusion to be present to conserve the integrity of the model fields.

The GM parameterization was then added to the GFDL code in the form of a non-divergent bolus velocity. The method defines two stream-functions expressed in terms of the isoneutral slopes subject to the boundary condition of zero value on upper and lower boundaries. The horizontal bolus velocities are then the vertical derivative of these functions. Here in lies a problem highlighted by Griffies et al. [1998]: the bolus velocities involve multiple derivatives on the potential density field, which can consequently give rise to noise. Griffies et al. point out that the GM bolus fluxes can be identically written as a skew flux which involves fewer differential operators. Further, combining the skew flux formulation and Redi scheme, substantial cancellations take place to the point that the horizontal fluxes are unmodified from the lateral diffusion parameterization.

6.4.1.1 Redi scheme: Isopycnal diffusion

The Redi scheme diffuses tracers along isopycnals and introduces a term in the tendency (rhs) of such a tracer (here $ \tau$ ) of the form:

$\displaystyle \bf {\nabla} \cdot \kappa_\rho \bf {K}_{Redi} \bf {\nabla} \tau$ (6.1)

where $ \kappa_\rho$ is the along isopycnal diffusivity and $ \bf {K}_{Redi}$ is a rank 2 tensor that projects the gradient of $ \tau$ onto the isopycnal surface. The unapproximated projection tensor is:

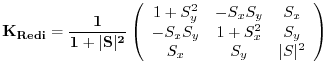$\displaystyle \bf {K}_{Redi} = \frac{1}{1 + \vert S\vert^2} \left( \begin{array... ...-S_x S_y & 1 + S_x^2 & S_y \\ S_x & S_y & \vert S\vert^2 \\ \end{array} \right)$ (6.2)

Here, $ S_x = -\partial_x \sigma / \partial_z \sigma$ and $ S_y = -\partial_y \sigma / \partial_z \sigma$ are the components of the isoneutral slope.

The first point to note is that a typical slope in the ocean interior is small, say of the order $ 10^{-4}$ . A maximum slope might be of order $ 10^{-2}$ and only exceeds such in unstratified regions where the slope is ill defined. It is therefore justifiable, and customary, to make the small slope approximation, $ \vert S\vert << 1$ . The Redi projection tensor then becomes:

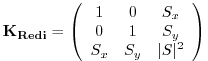$\displaystyle \bf {K}_{Redi} = \left( \begin{array}{ccc} 1 & 0 & S_x \\ 0 & 1 & S_y \\ S_x & S_y & \vert S\vert^2 \\ \end{array} \right)$ (6.3)

6.4.1.2 GM parameterization

The GM parameterization aims to represent the ``advective'' or ``transport'' effect of geostrophic eddies by means of a ``bolus'' velocity, $ \bf {u}^\star$ . The divergence of this advective flux is added to the tracer tendency equation (on the rhs):

$\displaystyle - \bf {\nabla} \cdot \tau \bf {u}^\star$ (6.4)

The bolus velocity $ \bf {u}^\star$ is defined as the rotational of a streamfunction $ \bf {F}^\star$ = $ (F_x^\star,F_y^\star,0)$ :

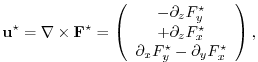$\displaystyle \bf {u}^\star = \nabla \times \bf {F}^\star = \left( \begin{array... ...z F_x^\star \\ \partial_x F_y^\star - \partial_y F_x^\star \end{array} \right),$ (6.5)

and thus is automatically non-divergent. In the GM parameterization, the streamfunction is specified in terms of the isoneutral slopes $ S_x$ and $ S_y$ :
$\displaystyle F_x^\star$ $\displaystyle =$ $\displaystyle -\kappa_{GM} S_y$ (6.6)
$\displaystyle F_y^\star$ $\displaystyle =$ $\displaystyle \kappa_{GM} S_x$ (6.7)

with boundary conditions $ F_x^\star=F_y^\star=0$ on upper and lower boundaries. In the end, the bolus transport in the GM parameterization is given by:

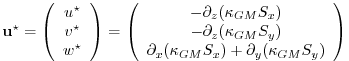$\displaystyle \bf {u}^\star = \left( \begin{array}{c} u^\star \\ v^\star \\ w^\... ...\partial_x (\kappa_{GM} S_x) + \partial_y (\kappa_{GM} S_y) \end{array} \right)$ (6.8)

This is the form of the GM parameterization as applied by Donabasaglu, 1997, in MOM versions 1 and 2.

Note that in the MITgcm, the variables containing the GM bolus streamfunction are:

$\displaystyle \left( \begin{array}{c} GM\_PsiX \\ GM\_PsiY \end{array} \right) ... ...} \right)= \left( \begin{array}{c} F_y^\star \\ -F_x^\star \end{array} \right).$ (6.9)

6.4.1.3 Griffies Skew Flux

Griffies [1998] notes that the discretisation of bolus velocities involves multiple layers of differencing and interpolation that potentially lead to noisy fields and computational modes. He pointed out that the bolus flux can be re-written in terms of a non-divergent flux and a skew-flux:

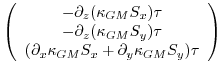$\displaystyle \bf {u}^\star \tau$ $\displaystyle =$ $\displaystyle \left( \begin{array}{c} - \partial_z ( \kappa_{GM} S_x ) \tau \\ ... ...partial_x \kappa_{GM} S_x + \partial_y \kappa_{GM} S_y)\tau \end{array} \right)$  
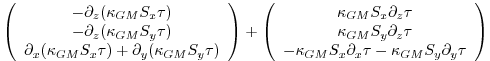  $\displaystyle =$ $\displaystyle \left( \begin{array}{c} - \partial_z ( \kappa_{GM} S_x \tau) \\ ... ..._{GM} S_x \partial_x \tau - \kappa_{GM} S_y \partial_y \tau \end{array} \right)$  

The first vector is non-divergent and thus has no effect on the tracer field and can be dropped. The remaining flux can be written:

$\displaystyle \bf {u}^\star \tau = - \kappa_{GM} \bf {K}_{GM} \bf {\nabla} \tau$ (6.10)

where

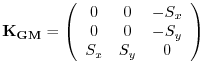$\displaystyle \bf {K}_{GM} = \left( \begin{array}{ccc} 0 & 0 & -S_x \\ 0 & 0 & -S_y \\ S_x & S_y & 0 \end{array} \right)$ (6.11)

is an anti-symmetric tensor.

This formulation of the GM parameterization involves fewer derivatives than the original and also involves only terms that already appear in the Redi mixing scheme. Indeed, a somewhat fortunate cancellation becomes apparent when we use the GM parameterization in conjunction with the Redi isoneutral mixing scheme:

$\displaystyle \kappa_\rho \bf {K}_{Redi} \bf {\nabla} \tau - u^\star \tau = ( \kappa_\rho \bf {K}_{Redi} + \kappa_{GM} \bf {K}_{GM} ) \bf {\nabla} \tau$ (6.12)

In the instance that $ \kappa_{GM} = \kappa_{\rho}$ then

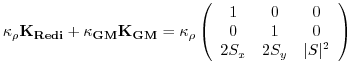$\displaystyle \kappa_\rho \bf {K}_{Redi} + \kappa_{GM} \bf {K}_{GM} = \kappa_\r... ...c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 2 S_x & 2 S_y & \vert S\vert^2 \end{array} \right)$ (6.13)

which differs from the variable Laplacian diffusion tensor by only two non-zero elements in the $ z$ -row.

\fbox{ \begin{minipage}{4.75in} {\em S/R GMREDI\_CALC\_TENSOR} ({\em pkg/gmredi/... ...ument on exit) \par $S_y$: {\bf SlopeY} (argument on exit) \par \end{minipage} }

6.4.1.4 Variable $ \kappa _{GM}$

Visbeck et al. [1997] suggest making the eddy coefficient, $ \kappa _{GM}$ , a function of the Eady growth rate, $ \vert f\vert/\sqrt{Ri}$ . The formula involves a non-dimensional constant, $ \alpha $ , and a length-scale $ L$ :

$\displaystyle \kappa_{GM} = \alpha L^2 \overline{ \frac{\vert f\vert}{\sqrt{Ri}} }^z $

where the Eady growth rate has been depth averaged (indicated by the over-line). A local Richardson number is defined $ Ri = N^2 / (\partial u/\partial z)^2$ which, when combined with thermal wind gives:

$\displaystyle \frac{1}{Ri} = \frac{(\frac{\partial u}{\partial z})^2}{N^2} = \f... ...\vert {\bf\nabla} \sigma \vert )^2 }{N^2} = \frac{ M^4 }{ \vert f\vert^2 N^2 } $

where $ M^2$ is defined $ M^2 = \frac{g}{\rho_o} \vert{\bf\nabla} \sigma\vert$ . Substituting into the formula for $ \kappa _{GM}$ gives:

$\displaystyle \kappa_{GM} = \alpha L^2 \overline{ \frac{M^2}{N} }^z = \alpha L^2 \overline{ \frac{M^2}{N^2} N }^z = \alpha L^2 \overline{ \vert S\vert N }^z $

6.4.1.5 Tapering and stability

Experience with the GFDL model showed that the GM scheme has to be matched to the convective parameterization. This was originally expressed in connection with the introduction of the KPP boundary layer scheme [Large et al., 1994] but in fact, as subsequent experience with the MIT model has found, is necessary for any convective parameterization.

\fbox{ \begin{minipage}{4.75in} {\em S/R GMREDI\_SLOPE\_LIMIT} ({\em pkg/gmredi/... ...rgument) \par $z_\sigma^{*}$: {\bf dRdSigmaLtd} (argument) \par \end{minipage} }

Figure 6.6: Taper functions used in GKW91 and DM95.
\resizebox{5.0in}{3.0in}{\includegraphics{s_phys_pkgs/figs/tapers.eps}}

Figure 6.7: Effective slope as a function of ``true'' slope using Cox slope clipping, GKW91 limiting and DM95 limiting.
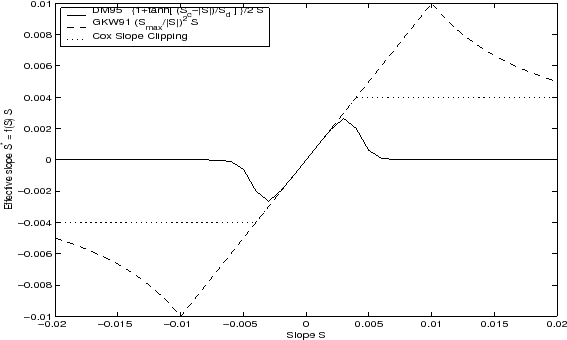
\resizebox{5.0in}{3.0in}{\includegraphics{s_phys_pkgs/figs/effective_slopes.eps}}

Slope clipping

Deep convection sites and the mixed layer are indicated by homogenized, unstable or nearly unstable stratification. The slopes in such regions can be either infinite, very large with a sign reversal or simply very large. From a numerical point of view, large slopes lead to large variations in the tensor elements (implying large bolus flow) and can be numerically unstable. This was first recognized by Cox [1987] who implemented ``slope clipping'' in the isopycnal mixing tensor. Here, the slope magnitude is simply restricted by an upper limit:

$\displaystyle \vert\nabla \sigma\vert$ $\displaystyle =$ $\displaystyle \sqrt{ \sigma_x^2 + \sigma_y^2 }$ (6.14)
$\displaystyle S_{lim}$ $\displaystyle =$ $\displaystyle - \frac{\vert\nabla \sigma\vert}{ S_{max} } \;\;\;\;\;\;\;\;$   $\displaystyle \mbox{where $S_{max}$\ is a parameter}$ (6.15)
$\displaystyle \sigma_z^\star$ $\displaystyle =$ $\displaystyle \min( \sigma_z , S_{lim} )$ (6.16)
$\displaystyle {[s_x,s_y]}$ $\displaystyle =$ $\displaystyle - \frac{ [\sigma_x,\sigma_y] }{\sigma_z^\star}$ (6.17)

Notice that this algorithm assumes stable stratification through the ``min'' function. In the case where the fluid is well stratified ( $ \sigma_z < S_{lim}$ ) then the slopes evaluate to:

$\displaystyle {[s_x,s_y]} = - \frac{ [\sigma_x,\sigma_y] }{\sigma_z}$ (6.18)

while in the limited regions ( $ \sigma_z > S_{lim}$ ) the slopes become:

$\displaystyle {[s_x,s_y]} = \frac{ [\sigma_x,\sigma_y] }{\vert\nabla \sigma\vert/S_{max}}$ (6.19)

so that the slope magnitude is limited $ \sqrt{s_x^2 + s_y^2} = S_{max}$ .

The slope clipping scheme is activated in the model by setting GM_taper_scheme = 'clipping' in data.gmredi.

Even using slope clipping, it is normally the case that the vertical diffusion term (with coefficient $ \kappa_\rho{\bf K}_{33} = \kappa_\rho S_{max}^2$ ) is large and must be time-stepped using an implicit procedure (see section on discretisation and code later). Fig. 6.8 shows the mixed layer depth resulting from a) using the GM scheme with clipping and b) no GM scheme (horizontal diffusion). The classic result of dramatically reduced mixed layers is evident. Indeed, the deep convection sites to just one or two points each and are much shallower than we might prefer. This, it turns out, is due to the over zealous re-stratification due to the bolus transport parameterization. Limiting the slopes also breaks the adiabatic nature of the GM/Redi parameterization, re-introducing diabatic fluxes in regions where the limiting is in effect.

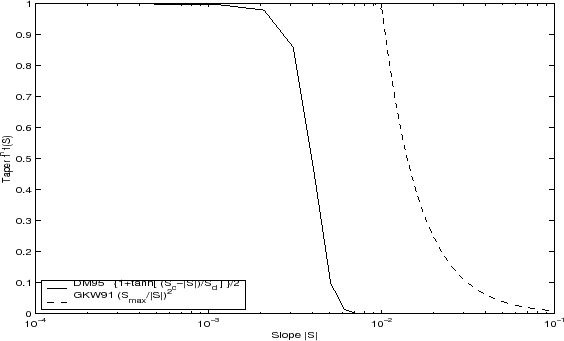
Tapering: Gerdes, Koberle and Willebrand, Clim. Dyn. 1991

The tapering scheme used in Gerdes et al. [1991] addressed two issues with the clipping method: the introduction of large vertical fluxes in addition to convective adjustment fluxes is avoided by tapering the GM/Redi slopes back to zero in low-stratification regions; the adjustment of slopes is replaced by a tapering of the entire GM/Redi tensor. This means the direction of fluxes is unaffected as the amplitude is scaled.

The scheme inserts a tapering function, $ f_1(S)$ , in front of the GM/Redi tensor:

$\displaystyle f_1(S) = \min \left[ 1, \left( \frac{S_{max}}{\vert S\vert}\right)^2 \right]$ (6.20)

where $ S_{max}$ is the maximum slope you want allowed. Where the slopes, $ \vert S\vert<S_{max}$ then $ f_1(S) = 1$ and the tensor is un-tapered but where $ \vert S\vert \ge S_{max}$ then $ f_1(S)$ scales down the tensor so that the effective vertical diffusivity term $ \kappa f_1(S) \vert S\vert^2 = \kappa S_{max}^2$ .

The GKW91 tapering scheme is activated in the model by setting GM_taper_scheme = 'gkw91' in data.gmredi.

Tapering: Danabasoglu and McWilliams, J. Clim. 1995

The tapering scheme used by Danabasoglu and McWilliams [1995] followed a similar procedure but used a different tapering function, $ f_1(S)$ :

$\displaystyle f_1(S) = \frac{1}{2} \left( 1+\tanh \left[ \frac{S_c - \vert S\vert}{S_d} \right] \right)$ (6.21)

where $ S_c = 0.004$ is a cut-off slope and $ S_d=0.001$ is a scale over which the slopes are smoothly tapered. Functionally, the operates in the same way as the GKW91 scheme but has a substantially lower cut-off, turning off the GM/Redi SGS parameterization for weaker slopes.

The DM95 tapering scheme is activated in the model by setting GM_taper_scheme = 'dm95' in data.gmredi.

Tapering: Large, Danabasoglu and Doney, JPO 1997

The tapering used in Large et al. [1997] is based on the DM95 tapering scheme, but also tapers the scheme with an additional function of height, $ f_2(z)$ , so that the GM/Redi SGS fluxes are reduced near the surface:

$\displaystyle f_2(z) = \frac{1}{2} \left( 1 + \sin(\pi \frac{z}{D} - \frac{\pi}{2})\right)$ (6.22)

where $ D = L_\rho \vert S\vert$ is a depth-scale and $ L_\rho=c/f$ with $ c=2$  m s$ ^{-1}$ . This tapering with height was introduced to fix some spurious interaction with the mixed-layer KPP parameterization.

The LDD97 tapering scheme is activated in the model by setting GM_taper_scheme = 'ldd97' in data.gmredi.

Figure 6.8: Mixed layer depth using GM parameterization with a) Cox slope clipping and for comparison b) using horizontal constant diffusion.
\begin{figure}\begin{center} Figure missing. \end{center} \end{figure}


6.4.1.6 Package Reference 

------------------------------------------------------------------------
<-Name->|Levs|<-parsing code->|<--  Units   -->|<- Tile (max=80c) 
------------------------------------------------------------------------
GM_VisbK|  1 |SM P    M1      |m^2/s           |Mixing coefficient from Visbeck etal parameterization
GM_Kux  | 15 |UU P 177MR      |m^2/s           |K_11 element (U.point, X.dir) of GM-Redi tensor
GM_Kvy  | 15 |VV P 176MR      |m^2/s           |K_22 element (V.point, Y.dir) of GM-Redi tensor
GM_Kuz  | 15 |UU   179MR      |m^2/s           |K_13 element (U.point, Z.dir) of GM-Redi tensor
GM_Kvz  | 15 |VV   178MR      |m^2/s           |K_23 element (V.point, Z.dir) of GM-Redi tensor
GM_Kwx  | 15 |UM   181LR      |m^2/s           |K_31 element (W.point, X.dir) of GM-Redi tensor
GM_Kwy  | 15 |VM   180LR      |m^2/s           |K_32 element (W.point, Y.dir) of GM-Redi tensor
GM_Kwz  | 15 |WM P    LR      |m^2/s           |K_33 element (W.point, Z.dir) of GM-Redi tensor
GM_PsiX | 15 |UU   184LR      |m^2/s           |GM Bolus transport stream-function : X component
GM_PsiY | 15 |VV   183LR      |m^2/s           |GM Bolus transport stream-function : Y component
GM_KuzTz| 15 |UU   186MR      |degC.m^3/s      |Redi Off-diagonal Tempetature flux: X component
GM_KvzTz| 15 |VV   185MR      |degC.m^3/s      |Redi Off-diagonal Tempetature flux: Y component


6.4.1.7 Experiments and tutorials that use gmredi

  • Global Ocean tutorial, in tutorial_global_oce_latlon verification directory, described in section 3.12
  • Front Relax experiment, in front_relax verification directory.
  • Ideal 2D Ocean experiment, in ideal_2D_oce verification directory.

next up previous contents
Next: 6.4.2 KPP: Nonlocal K-Profile Up: 6.4 Ocean Packages Previous: 6.4 Ocean Packages   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2018-01-23