|
 |
|||||||||||
 |
|
|||||||||||
 |
 |
|||||||||||
|
Next: 6.4.3 GGL90: a TKE Up: 6.4 Ocean Packages Previous: 6.4.1 GMREDI: Gent/McWiliams/Redi SGS Contents Subsections
6.4.2 KPP: Nonlocal K-Profile Parameterization for Vertical MixingAuthors: Dimitris Menemenlis and Patrick Heimbach
|
| implicitViscosity = .TRUE. | enable implicit vertical viscosity |
| implicitDiffusion = .TRUE. | enable implicit vertical diffusion |
6.4.2.3.3 Package flags and parameters
Table 6.4.2.3 summarizes the runtime flags that are set in data.pkg, and their default values.
6.4.2.4 Equations and key routines
We restrict ourselves to writing out only the essential equations that relate to main processes and parameters mentioned above. We closely follow the notation of Large et al. [1994].
6.4.2.4.1 KPP_CALC:
Top-level routine.
6.4.2.4.2 KPP_MIX:
Intermediate-level routine
6.4.2.4.3 BLMIX: Mixing in the boundary layer
The vertical fluxes
![]() of momentum and tracer properties
of momentum and tracer properties ![]() is composed of a gradient-flux term (proportional to
the vertical property divergence
is composed of a gradient-flux term (proportional to
the vertical property divergence
![]() ), and
a ``nonlocal'' term
), and
a ``nonlocal'' term ![]() that enhances the
gradient-flux mixing coefficient
that enhances the
gradient-flux mixing coefficient ![]()
| (6.23) |
- Boundary layer mixing profile
It is expressed as the product of the boundary layer depth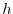 ,
a depth-dependent turbulent velocity scale
,
a depth-dependent turbulent velocity scale
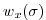 and a
non-dimensional shape function
and a
non-dimensional shape function 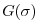
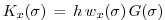
(6.24)
with dimensionless vertical coordinate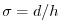 .
For details of
.
For details of
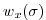 and
and 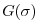 we refer to
Large et al. [1994].
we refer to
Large et al. [1994].
- Nonlocal mixing term
The nonlocal transport term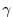 is nonzero only for
tracers in unstable (convective) forcing conditions.
Thus, depending on the stability parameter
is nonzero only for
tracers in unstable (convective) forcing conditions.
Thus, depending on the stability parameter
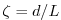 (with depth
(with depth 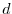 , Monin-Obukhov length scale
, Monin-Obukhov length scale 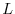 )
it has the following form:
)
it has the following form:
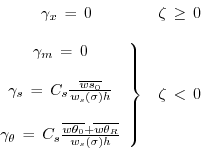
(6.25)
In practice, the routine peforms the following tasks:
- compute velocity scales at hbl
- find the interior viscosities and derivatives at hbl
- compute turbulent velocity scales on the interfaces
- compute the dimensionless shape functions at the interfaces
- compute boundary layer diffusivities at the interfaces
- compute nonlocal transport term
- find diffusivities at kbl-1 grid level
6.4.2.4.4 RI_IWMIX: Mixing in the interior
Compute interior viscosity and diffusivity coefficients due to
- shear instability (dependent on a local gradient Richardson number),
- to background internal wave activity, and
- to static instability (local Richardson number
 0).
0).
TO BE CONTINUED.
6.4.2.4.5 BLDEPTH: Boundary layer depth calculation:
The oceanic planetary boundary layer depth, hbl, is determined as the shallowest depth where the bulk Richardson number is equal to the critical value, Ricr.
Bulk Richardson numbers are evaluated by computing velocity and buoyancy differences between values at zgrid(kl) < 0 and surface reference values. In this configuration, the reference values are equal to the values in the surface layer. When using a very fine vertical grid, these values should be computed as the vertical average of velocity and buoyancy from the surface down to epsilon*zgrid(kl).
When the bulk Richardson number at k exceeds Ricr, hbl is linearly interpolated between grid levels zgrid(k) and zgrid(k-1).
The water column and the surface forcing are diagnosed for stable/ustable forcing conditions, and where hbl is relative to grid points (caseA), so that conditional branches can be avoided in later subroutines.
TO BE CONTINUED.
6.4.2.4.6 KPP_CALC_DIFF_T/_S, KPP_CALC_VISC:
Add contribution to net diffusivity/viscosity from KPP diffusivity/viscosity.
TO BE CONTINUED.
6.4.2.4.7 KPP_TRANSPORT_T/_S/_PTR:
Add non local KPP transport term (ghat) to diffusive temperature/salinity/passive tracer flux. The nonlocal transport term is nonzero only for scalars in unstable (convective) forcing conditions.
TO BE CONTINUED.
6.4.2.4.8 Implicit time integration
TO BE CONTINUED.
6.4.2.4.9 Penetration of shortwave radiation
TO BE CONTINUED.
6.4.2.5 Flow chart
C !CALLING SEQUENCE: c ... c kpp_calc (TOP LEVEL ROUTINE) c | c |-- statekpp: o compute all EOS/density-related arrays c | o uses S/R FIND_ALPHA, FIND_BETA, FIND_RHO c | c |-- kppmix c | |--- ri_iwmix (compute interior mixing coefficients due to constant c | | internal wave activity, static instability, c | | and local shear instability). c | | c | |--- bldepth (diagnose boundary layer depth) c | | c | |--- blmix (compute boundary layer diffusivities) c | | c | |--- enhance (enhance diffusivity at interface kbl - 1) c | o c | c |-- swfrac c o
6.4.2.6 KPP diagnostics
Diagnostics output is available via the diagnostics package (see Section 7.1). Available output fields are summarized here:
------------------------------------------------------ <-Name->|Levs|grid|<-- Units -->|<- Tile (max=80c) ------------------------------------------------------ KPPviscA| 23 |SM |m^2/s |KPP vertical eddy viscosity coefficient KPPdiffS| 23 |SM |m^2/s |Vertical diffusion coefficient for salt & tracers KPPdiffT| 23 |SM |m^2/s |Vertical diffusion coefficient for heat KPPghat | 23 |SM |s/m^2 |Nonlocal transport coefficient KPPhbl | 1 |SM |m |KPP boundary layer depth, bulk Ri criterion KPPmld | 1 |SM |m |Mixed layer depth, dT=.8degC density criterion KPPfrac | 1 |SM | |Short-wave flux fraction penetrating mixing layer
6.4.2.7 Reference experiments
lab_sea:
natl_box:
6.4.2.8 References
6.4.2.9 Experiments and tutorials that use kpp
- Labrador Sea experiment, in lab_sea verification directory
Next: 6.4.3 GGL90: a TKE Up: 6.4 Ocean Packages Previous: 6.4.1 GMREDI: Gent/McWiliams/Redi SGS Contents mitgcm-support@mitgcm.org