Home Contact Us Site Map  
 
       
    next up previous contents
Next: 6.6 Sea Ice Packages Up: 6.5 Atmosphere Packages Previous: 6.5.2 Land package   Contents

Subsections


6.5.3 Fizhi: High-end Atmospheric Physics

6.5.3.1 Introduction

The fizhi (high-end atmospheric physics) package includes a collection of state-of-the-art physical parameterizations for atmospheric radiation, cumulus convection, atmospheric boundary layer turbulence, and land surface processes. The collection of atmospheric physics parameterizations were originally used together as part of the GEOS-3 (Goddard Earth Observing System-3) GCM developed at the NASA/Goddard Global Modelling and Assimilation Office (GMAO).

6.5.3.2 Equations

Moist Convective Processes:


6.5.3.2.1 Sub-grid and Large-scale Convection

Sub-grid scale cumulus convection is parameterized using the Relaxed Arakawa Schubert (RAS) scheme of Moorthi and Suarez [1992], which is a linearized Arakawa Schubert type scheme. RAS predicts the mass flux from an ensemble of clouds. Each subensemble is identified by its entrainment rate and level of neutral bouyancy which are determined by the grid-scale properties.

The thermodynamic variables that are used in RAS to describe the grid scale vertical profile are the dry static energy, $ s=c_pT +gz$ , and the moist static energy, $ h=c_p T + gz + Lq$ . The conceptual model behind RAS depicts each subensemble as a rising plume cloud, entraining mass from the environment during ascent, and detraining all cloud air at the level of neutral buoyancy. RAS assumes that the normalized cloud mass flux, $ \eta $ , normalized by the cloud base mass flux, is a linear function of height, expressed as:

$\displaystyle \frac{\partial \eta(z)}{\partial z} = \lambda \hspace{0.4cm}or\hs... ...\partial \eta(P^{\kappa})}{\partial P^{\kappa}} = -\frac{c_p}{g}\theta\lambda $

where we have used the hydrostatic equation written in the form:

$\displaystyle \frac{\partial z}{\partial P^{\kappa}} = -\frac{c_p}{g}\theta $

The entrainment parameter, $ \lambda $ , characterizes a particular subensemble based on its detrainment level, and is obtained by assuming that the level of detrainment is the level of neutral buoyancy, ie., the level at which the moist static energy of the cloud, $ h_c$ , is equal to the saturation moist static energy of the environment, $ h^*$ . Following Moorthi and Suarez [1992], $ \lambda $ may be written as

$\displaystyle \lambda = \frac{h_B - h^*_D}{ \frac{c_p}{g} \int_{P_D}^{P_B}\theta(h^*_D-h)dP^{\kappa}}, $

where the subscript $ B$ refers to cloud base, and the subscript $ D$ refers to the detrainment level.

The convective instability is measured in terms of the cloud work function $ A$ , defined as the rate of change of cumulus kinetic energy. The cloud work function is related to the buoyancy, or the difference between the moist static energy in the cloud and in the environment:

$\displaystyle A = \int_{P_D}^{P_B} \frac{\eta}{1 + \gamma} \left[ \frac{h_c-h^*}{P^{\kappa}} \right] dP^{\kappa} $

where $ \gamma$ is $ \frac{L}{c_p}\frac{\partial q^*}{\partial T}$ obtained from the Claussius Clapeyron equation, and the subscript $ c$ refers to the value inside the cloud.

To determine the cloud base mass flux, the rate of change of $ A$ in time due to dissipation by the clouds is assumed to approximately balance the rate of change of $ A$ due to the generation by the large scale. This is the quasi-equilibrium assumption, and results in an expression for $ m_B$ :

$\displaystyle m_B = \frac{- \left. \frac{dA}{dt} \right\vert _{ls}}{K} $

where $ K$ is the cloud kernel, defined as the rate of change of the cloud work function per unit cloud base mass flux, and is currently obtained by analytically differentiating the expression for $ A$ in time. The rate of change of $ A$ due to the generation by the large scale can be written as the difference between the current $ A(t+\Delta t)$ and its equillibrated value after the previous convective time step $ A(t)$ , divided by the time step. $ A(t)$ is approximated as some critical $ A_{crit}$ , computed by Lord (1982) from $ in situ$ observations.

The predicted convective mass fluxes are used to solve grid-scale temperature and moisture budget equations to determine the impact of convection on the large scale fields of temperature (through latent heating and compensating subsidence) and moisture (through precipitation and detrainment):

$\displaystyle \left.{\frac{\partial \theta}{\partial t}}\right\vert _{c} = \alpha \frac{ m_B}{c_p P^{\kappa}} \eta \frac{\partial s}{\partial p} $

and

$\displaystyle \left.{\frac{\partial q}{\partial t}}\right\vert _{c} = \alpha \frac{ m_B}{L} \eta (\frac{\partial h}{\partial p}-\frac{\partial s}{\partial p}) $

where $ \theta = \frac{T}{P^{\kappa}}$ , $ P = (p/p_0)$ , and $ \alpha $ is the relaxation parameter.

As an approximation to a full interaction between the different allowable subensembles, many clouds are simulated frequently, each modifying the large scale environment some fraction $ \alpha $ of the total adjustment. The parameterization thereby ``relaxes'' the large scale environment towards equillibrium.

In addition to the RAS cumulus convection scheme, the fizhi package employs a Kessler-type scheme for the re-evaporation of falling rain (Sud and Molod [1988]), which correspondingly adjusts the temperature assuming $ h$ is conserved. RAS in its current formulation assumes that all cloud water is deposited into the detrainment level as rain. All of the rain is available for re-evaporation, which begins in the level below detrainment. The scheme accounts for some microphysics such as the rainfall intensity, the drop size distribution, as well as the temperature, pressure and relative humidity of the surrounding air. The fraction of the moisture deficit in any model layer into which the rain may re-evaporate is controlled by a free parameter, which allows for a relatively efficient re-evaporation of liquid precipitate and larger rainout for frozen precipitation.

Due to the increased vertical resolution near the surface, the lowest model layers are averaged to provide a 50 mb thick sub-cloud layer for RAS. Each time RAS is invoked (every ten simulated minutes), a number of randomly chosen subensembles are checked for the possibility of convection, from just above cloud base to 10 mb.

Supersaturation or large-scale precipitation is initiated in the fizhi package whenever the relative humidity in any grid-box exceeds a critical value, currently 100 %. The large-scale precipitation re-evaporates during descent to partially saturate lower layers in a process identical to the re-evaporation of convective rain.


6.5.3.2.2 Cloud Formation

Convective and large-scale cloud fractons which are used for cloud-radiative interactions are determined diagnostically as part of the cumulus and large-scale parameterizations. Convective cloud fractions produced by RAS are proportional to the detrained liquid water amount given by

$\displaystyle F_{RAS} = \min\left[ \frac{l_{RAS}}{l_c}, 1.0 \right] $

where $ l_c$ is an assigned critical value equal to $ 1.25$ g/kg. A memory is associated with convective clouds defined by:

$\displaystyle F_{RAS}^n = \min\left[ F_{RAS} + (1-\frac{\Delta t_{RAS}}{\tau})F_{RAS}^{n-1}, 1.0 \right] $

where $ F_{RAS}$ is the instantanious cloud fraction and $ F_{RAS}^{n-1}$ is the cloud fraction from the previous RAS timestep. The memory coefficient is computed using a RAS cloud timescale, $ \tau$ , equal to 1 hour. RAS cloud fractions are cleared when they fall below 5 %.

Large-scale cloudiness is defined, following Slingo and Ritter (1985), as a function of relative humidity:

$\displaystyle F_{LS} = \min\left[ { \left( \frac{RH-RH_c}{1-RH_c} \right) }^2, 1.0 \right] $

where


$\displaystyle RH_c$ $\displaystyle =$ $\displaystyle 1-s(1-s)(2-\sqrt{3}+2\sqrt{3} \, s)r$  
$\displaystyle s$ $\displaystyle =$ $\displaystyle p/p_{surf}$  
$\displaystyle r$ $\displaystyle =$ $\displaystyle \left( \frac{1.0-RH_{min}}{\alpha} \right)$  
$\displaystyle RH_{min}$ $\displaystyle =$ $\displaystyle 0.75$  
$\displaystyle \alpha$ $\displaystyle =$ $\displaystyle 0.573285 .$  

These cloud fractions are suppressed, however, in regions where the convective sub-cloud layer is conditionally unstable. The functional form of $ RH_c$ is shown in Figure (6.9).

\begin{figure*} % latex2html id marker 31586 \vspace{0.4in} \centerline{ \epsf... ...ive Humidity for Clouds.] {Critical Relative Humidity for Clouds.} \end{figure*}

The total cloud fraction in a grid box is determined by the larger of the two cloud fractions:

$\displaystyle F_{CLD} = \max \left[ F_{RAS},F_{LS} \right] . $

Finally, cloud fractions are time-averaged between calls to the radiation packages.

Radiation:

The parameterization of radiative heating in the fizhi package includes effects from both shortwave and longwave processes. Radiative fluxes are calculated at each model edge-level in both up and down directions. The heating rates/cooling rates are then obtained from the vertical divergence of the net radiative fluxes.

The net flux is

$\displaystyle F = F^\uparrow - F^\downarrow $

where $ F$ is the net flux, $ F^\uparrow$ is the upward flux and $ F^\downarrow$ is the downward flux.

The heating rate due to the divergence of the radiative flux is given by

$\displaystyle \frac{\partial \rho c_p T}{\partial t} = - \frac{\partial F}{\partial z} $

or

$\displaystyle \frac{\partial T}{\partial t} = \frac{g}{c_p \pi} \frac{\partial F}{\partial \sigma} $

where $ g$ is the accelation due to gravity and $ c_p$ is the heat capacity of air at constant pressure.

The time tendency for Longwave Radiation is updated every 3 hours. The time tendency for Shortwave Radiation is updated once every three hours assuming a normalized incident solar radiation, and subsequently modified at every model time step by the true incident radiation. The solar constant value used in the package is equal to 1365 $ W/m^2$ and a $ CO_2 $ mixing ratio of 330 ppm. For the ozone mixing ratio, monthly mean zonally averaged climatological values specified as a function of latitude and height (Rosenfield et al. [1987]) are linearly interpolated to the current time.

6.5.3.2.3 Shortwave Radiation

The shortwave radiation package used in the package computes solar radiative heating due to the absoption by water vapor, ozone, carbon dioxide, oxygen, clouds, and aerosols and due to the scattering by clouds, aerosols, and gases. The shortwave radiative processes are described by Chou [1990,1992]. This shortwave package uses the Delta-Eddington approximation to compute the bulk scattering properties of a single layer following King and Harshvardhan (JAS, 1986). The transmittance and reflectance of diffuse radiation follow the procedures of Sagan and Pollock (JGR, 1967) and Lacis and Hansen [1974].

Highly accurate heating rate calculations are obtained through the use of an optimal grouping strategy of spectral bands. By grouping the UV and visible regions as indicated in Table 6.11, the Rayleigh scattering and the ozone absorption of solar radiation can be accurately computed in the ultraviolet region and the photosynthetically active radiation (PAR) region. The computation of solar flux in the infrared region is performed with a broadband parameterization using the spectrum regions shown in Table 6.12. The solar radiation algorithm used in the fizhi package can be applied not only for climate studies but also for studies on the photolysis in the upper atmosphere and the photosynthesis in the biosphere.


Table 6.11: UV and Visible Spectral Regions used in shortwave radiation package.
UV and Visible Spectral Regions


Region Band Wavelength (micron)
UV-C 1. .175 - .225
  2. .225 - .245
    .260 - .280
  3. .245 - .260
UV-B 4. .280 - .295
  5. .295 - .310
  6. .310 - .320
UV-A 7. .320 - .400
PAR 8. .400 - .700



Table 6.12: Infrared Spectral Regions used in shortwave radiation package.
Infrared Spectral Regions


Band Wavenumber(cm$ ^{-1}$ ) Wavelength (micron)
1 1000-4400 2.27-10.0
2 4400-8200 1.22-2.27
3 8200-14300 0.70-1.22


Within the shortwave radiation package, both ice and liquid cloud particles are allowed to co-exist in any of the model layers. Two sets of cloud parameters are used, one for ice paticles and the other for liquid particles. Cloud parameters are defined as the cloud optical thickness and the effective cloud particle size. In the fizhi package, the effective radius for water droplets is given as 10 microns, while 65 microns is used for ice particles. The absorption due to aerosols is currently set to zero.

To simplify calculations in a cloudy atmosphere, clouds are grouped into low ($ p>700$ mb), middle (700 mb $ \ge p > 400$ mb), and high ($ p < 400$ mb) cloud regions. Within each of the three regions, clouds are assumed maximally overlapped, and the cloud cover of the group is the maximum cloud cover of all the layers in the group. The optical thickness of a given layer is then scaled for both the direct (as a function of the solar zenith angle) and diffuse beam radiation so that the grouped layer reflectance is the same as the original reflectance. The solar flux is computed for each of eight cloud realizations possible within this low/middle/high classification, and appropriately averaged to produce the net solar flux.

6.5.3.2.4 Longwave Radiation

The longwave radiation package used in the fizhi package is thoroughly described by Chou and M.J.Suarez [1994]. As described in that document, IR fluxes are computed due to absorption by water vapor, carbon dioxide, and ozone. The spectral bands together with their absorbers and parameterization methods, configured for the fizhi package, are shown in Table 6.13.


Table 6.13: IR Spectral Bands, Absorbers, and Parameterization Method (from Chou and M.J.Suarez [1994])
IR Spectral Bands


Band Spectral Range (cm$ ^{-1}$ ) Absorber Method
1 0-340 H$ _2$ O line T
2 340-540 H$ _2$ O line T
3a 540-620 H$ _2$ O line K
3b 620-720 H$ _2$ O continuum S
3b 720-800 CO$ _2$ T
4 800-980 H$ _2$ O line K
    H$ _2$ O continuum S
    H$ _2$ O line K
5 980-1100 H$ _2$ O continuum S
    O$ _3$ T
6 1100-1380 H$ _2$ O line K
    H$ _2$ O continuum S
7 1380-1900 H$ _2$ O line T
8 1900-3000 H$ _2$ O line K
    K: k-distribution method with linear pressure scaling
    T: Table look-up with temperature and pressure scaling
    S: One-parameter temperature scaling



The longwave radiation package accurately computes cooling rates for the middle and lower atmosphere from 0.01 mb to the surface. Errors are $ <$ 0.4 C day$ ^{-1}$ in cooling rates and $ <$ 1% in fluxes. From Chou and Suarez, it is estimated that the total effect of neglecting all minor absorption bands and the effects of minor infrared absorbers such as nitrous oxide (N$ _2$ O), methane (CH$ _4$ ), and the chlorofluorocarbons (CFCs), is an underestimate of $ \approx$ 5 W/m$ ^2$ in the downward flux at the surface and an overestimate of $ \approx$ 3 W/m$ ^2$ in the upward flux at the top of the atmosphere.

Similar to the procedure used in the shortwave radiation package, clouds are grouped into three regions catagorized as low/middle/high. The net clear line-of-site probability $ (P)$ between any two levels, $ p_1$ and $ p_2 \quad (p_2 > p_1)$ , assuming randomly overlapped cloud groups, is simply the product of the probabilities within each group:

$\displaystyle P_{net} = P_{low} \times P_{mid} \times P_{hi} . $

Since all clouds within a group are assumed maximally overlapped, the clear line-of-site probability within a group is given by:

$\displaystyle P_{group} = 1 - F_{max} , $

where $ F_{max}$ is the maximum cloud fraction encountered between $ p_1$ and $ p_2$ within that group. For groups and/or levels outside the range of $ p_1$ and $ p_2$ , a clear line-of-site probability equal to 1 is assigned.


6.5.3.2.5 Cloud-Radiation Interaction

The cloud fractions and diagnosed cloud liquid water produced by moist processes within the fizhi package are used in the radiation packages to produce cloud-radiative forcing. The cloud optical thickness associated with large-scale cloudiness is made proportional to the diagnosed large-scale liquid water, $ \ell$ , detrained due to super-saturation. Two values are used corresponding to cloud ice particles and water droplets. The range of optical thickness for these clouds is given as

$\displaystyle 0.0002 \le \tau_{ice} (mb^{-1}) \le 0.002$   for$\displaystyle \quad 0 \le \ell \le 2$   mg/kg$\displaystyle ,$

$\displaystyle 0.02 \le \tau_{h_2o} (mb^{-1}) \le 0.2$   for$\displaystyle \quad 0 \le \ell \le 10$   mg/kg$\displaystyle . $

The partitioning, $ \alpha $ , between ice particles and water droplets is achieved through a linear scaling in temperature:

$\displaystyle 0 \le \alpha \le 1$   for$\displaystyle \quad 233.15 \le T \le 253.15 . $

The resulting optical depth associated with large-scale cloudiness is given as

$\displaystyle \tau_{LS} = \alpha \tau_{h_2o} + (1-\alpha)\tau_{ice} . $

The optical thickness associated with sub-grid scale convective clouds produced by RAS is given as

$\displaystyle \tau_{RAS} = 0.16 \quad mb^{-1} . $

The total optical depth in a given model layer is computed as a weighted average between the large-scale and sub-grid scale optical depths, normalized by the total cloud fraction in the layer:

$\displaystyle \tau = \left( \frac{F_{RAS} \,\,\, \tau_{RAS} + F_{LS} \,\,\, \tau_{LS} }{ F_{RAS}+F_{LS} } \right) \Delta p, $

where $ F_{RAS}$ and $ F_{LS}$ are the time-averaged cloud fractions associated with RAS and large-scale processes described in Section 6.5.3.2. The optical thickness for the longwave radiative feedback is assumed to be 75 $ \%$ of these values.

The entire Moist Convective Processes Module is called with a frequency of 10 minutes. The cloud fraction values are time-averaged over the period between Radiation calls (every 3 hours). Therefore, in a time-averaged sense, both convective and large-scale cloudiness can exist in a given grid-box.

6.5.3.2.6 Turbulence

:

Turbulence is parameterized in the fizhi package to account for its contribution to the vertical exchange of heat, moisture, and momentum. The turbulence scheme is invoked every 30 minutes, and employs a backward-implicit iterative time scheme with an internal time step of 5 minutes. The tendencies of atmospheric state variables due to turbulent diffusion are calculated using the diffusion equations:

$\displaystyle {\frac{\partial u}{\partial t}}_{turb} = {\frac{\partial }{\parti... ...me}})} = {\frac{\partial }{\partial z} }{(K_m \frac{\partial u}{\partial z})} $

$\displaystyle {\frac{\partial v}{\partial t}}_{turb} = {\frac{\partial }{\parti... ...me}})} = {\frac{\partial }{\partial z} }{(K_m \frac{\partial v}{\partial z})} $

$\displaystyle {\frac{\partial T}{\partial t}} = P^{\kappa}{\frac{\partial \thet... ...pa}{\frac{\partial }{\partial z} }{(K_h \frac{\partial \theta_v}{\partial z})} $

$\displaystyle {\frac{\partial q}{\partial t}}_{turb} = {\frac{\partial }{\parti... ...me}})} = {\frac{\partial }{\partial z} }{(K_h \frac{\partial q}{\partial z})} $

Within the atmosphere, the time evolution of second turbulent moments is explicitly modeled by representing the third moments in terms of the first and second moments. This approach is known as a second-order closure modeling. To simplify and streamline the computation of the second moments, the level 2.5 assumption of Mellor and Yamada (1974) and Yamada [1977] is employed, in which only the turbulent kinetic energy (TKE),

$\displaystyle { \frac{1}{2} }{q^2}={\overline{{u^{\prime}}^2}}+{\overline{{v^{\prime}}^2}}+{\overline{{w^{\prime}}^2}}, $

is solved prognostically and the other second moments are solved diagnostically. The prognostic equation for TKE allows the scheme to simulate some of the transient and diffusive effects in the turbulence. The TKE budget equation is solved numerically using an implicit backward computation of the terms linear in $ q^2$ and is written:

$\displaystyle {\frac{d }{d t} ({{ \frac{1}{2} } q^2})} - { \frac{\partial }{\pa... ...}{\overline{{w^{\prime}}{{{\theta}_v}^{\prime}}}} - \frac{ q^3}{{\Lambda}_1} } $

where $ q$ is the turbulent velocity, $ {u^{\prime}}$ , $ {v^{\prime}}$ , $ {w^{\prime}}$ and $ {{\theta}^{\prime}}$ are the fluctuating parts of the velocity components and potential temperature, $ U$ and $ V$ are the mean velocity components, $ {\Theta_0}^{-1}$ is the coefficient of thermal expansion, and $ {{\lambda}_1}$ and $ {{\Lambda} _1}$ are constant multiples of the master length scale, $ \ell$ , which is designed to be a characteristic measure of the vertical structure of the turbulent layers.

The first term on the left-hand side represents the time rate of change of TKE, and the second term is a representation of the triple correlation, or turbulent transport term. The first three terms on the right-hand side represent the sources of TKE due to shear and bouyancy, and the last term on the right hand side is the dissipation of TKE.

In the level 2.5 approach, the vertical fluxes of the scalars $ \theta_v$ and $ q$ and the wind components $ u$ and $ v$ are expressed in terms of the diffusion coefficients $ K_h$ and $ K_m$ , respectively. In the statisically realizable level 2.5 turbulence scheme of Helfand and Labraga [1988], these diffusion coefficients are expressed as

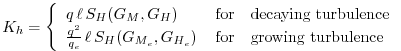
$\displaystyle K_h = \left\{ \begin{array}{l@{\quad\mbox{for}\quad}l} q \, \el... ...l \, S_{H}(G_{M_e},G_{H_e}) \, & \mbox{growing turbulence} \end{array} \right. $

and

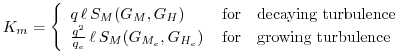
$\displaystyle K_m = \left\{ \begin{array}{l@{\quad\mbox{for}\quad}l} q \, \ell... ...l \, S_{M}(G_{M_e},G_{H_e}) \, & \mbox{growing turbulence} \end{array} \right. $

where the subscript $ e$ refers to the value under conditions of local equillibrium (obtained from the Level 2.0 Model), $ \ell$ is the master length scale related to the vertical structure of the atmosphere, and $ S_M$ and $ S_H$ are functions of $ G_H$ and $ G_M$ , the dimensionless buoyancy and wind shear parameters, respectively. Both $ G_H$ and $ G_M$ , and their equilibrium values $ G_{H_e}$ and $ G_{M_e}$ , are functions of the Richardson number:

$\displaystyle {\bf RI} = \frac{ \frac{g}{\theta_v} \frac{\partial \theta_v}{\pa... ...} }{ (\frac{\partial u}{\partial z})^2 + (\frac{\partial v}{\partial z})^2 } . $

Negative values indicate unstable buoyancy and shear, small positive values ($ <0.2$ ) indicate dominantly unstable shear, and large positive values indicate dominantly stable stratification.

Turbulent eddy diffusion coefficients of momentum, heat and moisture in the surface layer, which corresponds to the lowest GCM level (see -- missing table --), are calculated using stability-dependant functions based on Monin-Obukhov theory:

$\displaystyle {K_m} (surface) = C_u \times u_* = C_D W_s $

and

$\displaystyle {K_h} (surface) = C_t \times u_* = C_H W_s $

where $ u_*=C_uW_s$ is the surface friction velocity, $ C_D$ is termed the surface drag coefficient, $ C_H$ the heat transfer coefficient, and $ W_s$ is the magnitude of the surface layer wind.

$ C_u$ is the dimensionless exchange coefficient for momentum from the surface layer similarity functions:

$\displaystyle {C_u} = \frac{u_* }{ W_s} = \frac{ k }{ \psi_{m} } $

where k is the Von Karman constant and $ \psi_m$ is the surface layer non-dimensional wind shear given by

$\displaystyle \psi_{m} = {\int_{\zeta_{0}}^{\zeta} \frac{\phi_{m} }{ \zeta} d \zeta} . $

Here $ \zeta$ is the non-dimensional stability parameter, and $ \phi_m$ is the similarity function of $ \zeta$ which expresses the stability dependance of the momentum gradient. The functional form of $ \phi_m$ is specified differently for stable and unstable layers.

$ C_t$ is the dimensionless exchange coefficient for heat and moisture from the surface layer similarity functions:

$\displaystyle {C_t} = -\frac{( \overline{w^{\prime}\theta^{\prime}}) }{ u_* \De... ...w^{\prime}q^{\prime}}) }{ u_* \Delta q } = \frac{ k }{ (\psi_{h} + \psi_{g}) } $

where $ \psi_h$ is the surface layer non-dimensional temperature gradient given by

$\displaystyle \psi_{h} = {\int_{\zeta_{0}}^{\zeta} \frac{\phi_{h} }{ \zeta} d \zeta} . $

Here $ \phi_h$ is the similarity function of $ \zeta$ , which expresses the stability dependance of the temperature and moisture gradients, and is specified differently for stable and unstable layers according to Helfand and Schubert [1995].

$ \psi_g$ is the non-dimensional temperature or moisture gradient in the viscous sublayer, which is the mosstly laminar region between the surface and the tops of the roughness elements, in which temperature and moisture gradients can be quite large. Based on Yaglom and Kader [1974]:

$\displaystyle \psi_{g} = \frac{ 0.55 (Pr^{2/3} - 0.2) }{ \nu^{1/2} } (h_{0}u_{*} - h_{0_{ref}}u_{*_{ref}})^{1/2} $

where Pr is the Prandtl number for air, $ \nu$ is the molecular viscosity, $ z_{0}$ is the surface roughness length, and the subscript ref refers to a reference value. $ h_{0} = 30z_{0}$ with a maximum value over land of 0.01

The surface roughness length over oceans is is a function of the surface-stress velocity,

$\displaystyle {z_0} = c_1u^3_* + c_2u^2_* + c_3u_* + c_4 + \frac{c_5 }{ u_*} $

where the constants are chosen to interpolate between the reciprocal relation of Kondo [1975] for weak winds, and the piecewise linear relation of Large and Pond [1981] for moderate to large winds. Roughness lengths over land are specified from the climatology of Dorman and Sellers [1989].

For an unstable surface layer, the stability functions, chosen to interpolate between the condition of small values of $ \beta$ and the convective limit, are the KEYPS function (Panofsky [1973]) for momentum, and its generalization for heat and moisture:

$\displaystyle {\phi_m}^4 - 18 \zeta {\phi_m}^3 = 1 \hspace{1cm} ; \hspace{1cm} {\phi_h}^2 - 18 \zeta {\phi_h}^3 = 1 \hspace{1cm} . $

The function for heat and moisture assures non-vanishing heat and moisture fluxes as the wind speed approaches zero.

For a stable surface layer, the stability functions are the observationally based functions of Clarke [1970], slightly modified for the momemtum flux:

$\displaystyle {\phi_m} = \frac{ 1 + 5 {{\zeta}_1} }{ 1 + 0.00794 {\zeta}_1 (1+ ... ...hi_h} = \frac{ 1 + 5 {{\zeta}_1} }{ 1 + 0.00794 {\zeta} (1+ 5 {{\zeta}_1}) } . $

The moisture flux also depends on a specified evapotranspiration coefficient, set to unity over oceans and dependant on the climatological ground wetness over land.

Once all the diffusion coefficients are calculated, the diffusion equations are solved numerically using an implicit backward operator.

6.5.3.2.7 Atmospheric Boundary Layer

The depth of the atmospheric boundary layer (ABL) is diagnosed by the parameterization as the level at which the turbulent kinetic energy is reduced to a tenth of its maximum near surface value. The vertical structure of the ABL is explicitly resolved by the lowest few (3-8) model layers.

6.5.3.2.8 Surface Energy Budget

The ground temperature equation is solved as part of the turbulence package using a backward implicit time differencing scheme:

$\displaystyle C_g\frac{\partial T_g}{\partial t} = R_{sw} - R_{lw} + Q_{ice} - H - LE $

where $ R_{sw}$ is the net surface downward shortwave radiative flux and $ R_{lw}$ is the net surface upward longwave radiative flux.

$ H$ is the upward sensible heat flux, given by:

$\displaystyle {H} = P^{\kappa}\rho c_{p} C_{H} W_s (\theta_{surface} - \theta_{NLAY}) \hspace{1cm}where: \hspace{.2cm}C_H = C_u C_t $

where $ \rho $ = the atmospheric density at the surface, $ c_{p}$ is the specific heat of air at constant pressure, and $ \theta $ represents the potential temperature of the surface and of the lowest $ \sigma $ -level, respectively.

The upward latent heat flux, $ LE$ , is given by

$\displaystyle {LE} = \rho \beta L C_{H} W_s (q_{surface} - q_{NLAY}) \hspace{1cm}where: \hspace{.2cm}C_H = C_u C_t $

where $ \beta$ is the fraction of the potential evapotranspiration actually evaporated, L is the latent heat of evaporation, and $ q_{surface}$ and $ q_{NLAY}$ are the specific humidity of the surface and of the lowest $ \sigma $ -level, respectively.

The heat conduction through sea ice, $ Q_{ice}$ , is given by

$\displaystyle {Q_{ice}} = \frac{C_{ti} }{ H_i} (T_i-T_g) $

where $ C_{ti}$ is the thermal conductivity of ice, $ H_i$ is the ice thickness, assumed to be $ 3 \hspace{.1cm} m$ where sea ice is present, $ T_i$ is 273 degrees Kelvin, and $ T_g$ is the surface temperature of the ice.

$ C_g$ is the total heat capacity of the ground, obtained by solving a heat diffusion equation for the penetration of the diurnal cycle into the ground (Blackadar [1977]), and is given by:

$\displaystyle C_g = \sqrt{ \frac{\lambda C_s }{ 2\omega} } = \sqrt{(0.386 + 0.536W + 0.15W^2)2\times10^{-3} \frac{86400}{2\pi} } \, \, . $

Here, the thermal conductivity, $ \lambda $ , is equal to $ 2\times10^{-3}$ $ \frac{ly}{sec} \frac{cm}{K}$ , the angular velocity of the earth, $ \omega$ , is written as $ 86400$ $ sec/day$ divided by $ 2 \pi$ $ radians/ day$ , and the expression for $ C_s$ , the heat capacity per unit volume at the surface, is a function of the ground wetness, $ W$ .

Land Surface Processes:

6.5.3.2.9 Surface Type

The fizhi package surface Types are designated using the Koster-Suarez (Koster and Suarez [1992,1991]) Land Surface Model (LSM) mosaic philosophy which allows multiple ``tiles'', or multiple surface types, in any one grid cell. The Koster-Suarez LSM surface type classifications are shown in Table 6.14. The surface types and the percent of the grid cell occupied by any surface type were derived from the surface classification of Defries and Townshend [1994], and information about the location of permanent ice was obtained from the classifications of Dorman and Sellers [1989]. The surface type map for a $ 1^\circ$ grid is shown in Figure 6.10. The determination of the land or sea category of surface type was made from NCAR's 10 minute by 10 minute Navy topography dataset, which includes information about the percentage of water-cover at any point. The data were averaged to the model's grid resolutions, and any grid-box whose averaged water percentage was $ \geq 60 \%$ was defined as a water point. The Land-Water designation was further modified subjectively to ensure sufficient representation from small but isolated land and water regions.


Table 6.14: Surface type designations.
Surface Type Designation


Type Vegetation Designation
1 Broadleaf Evergreen Trees
2 Broadleaf Deciduous Trees
3 Needleleaf Trees
4 Ground Cover
5 Broadleaf Shrubs
6 Dwarf Trees (Tundra)
7 Bare Soil
8 Desert (Bright)
9 Glacier
10 Desert (Dark)
100 Ocean


Figure 6.10: Surface Type Combinations.
\begin{figure*}\centerline{ \epsfysize=4.0in \epsfbox{s_phys_pkgs/figs/surftype.eps}} \vspace{0.2in} \end{figure*}

6.5.3.2.10 Surface Roughness

The surface roughness length over oceans is computed iteratively with the wind stress by the surface layer parameterization (Helfand and Schubert [1995]). It employs an interpolation between the functions of Large and Pond [1981] for high winds and of Kondo [1975] for weak winds.

6.5.3.2.11 Albedo

The surface albedo computation, described in Koster and Suarez [1991], employs the ``two stream'' approximation used in Sellers' (1987) Simple Biosphere (SiB) Model which distinguishes between the direct and diffuse albedos in the visible and in the near infra-red spectral ranges. The albedos are functions of the observed leaf area index (a description of the relative orientation of the leaves to the sun), the greenness fraction, the vegetation type, and the solar zenith angle. Modifications are made to account for the presence of snow, and its depth relative to the height of the vegetation elements.

6.5.3.2.12 Gravity Wave Drag

The fizhi package employs the gravity wave drag scheme of Zhou et al. [1995]). This scheme is a modified version of Vernekar et al. (1992), which was based on Alpert et al. (1988) and Helfand et al. (1987). In this version, the gravity wave stress at the surface is based on that derived by Pierrehumbert (1986) and is given by:

$\displaystyle \vert\vec{\tau}_{sfc}\vert = \frac{\rho U^3}{N \ell^*} \left( \frac{F_r^2}{1+F_r^2}\right) \, \, ,$ (6.33)

where $ F_r = N h /U$ is the Froude number, $ N $ is the Brunt - Väisälä frequency, $ U$ is the surface wind speed, $ h$ is the standard deviation of the sub-grid scale orography, and $ \ell^*$ is the wavelength of the monochromatic gravity wave in the direction of the low-level wind. A modification introduced by Zhou et al. allows for the momentum flux to escape through the top of the model, although this effect is small for the current 70-level model. The subgrid scale standard deviation is defined by $ h$ , and is not allowed to exceed 400 m.

The effects of using this scheme within a GCM are shown in Takacs and Suarez [1996]. Experiments using the gravity wave drag parameterization yielded significant and beneficial impacts on both the time-mean flow and the transient statistics of the a GCM climatology, and have eliminated most of the worst dynamically driven biases in the a GCM simulation. An examination of the angular momentum budget during climate runs indicates that the resulting gravity wave torque is similar to the data-driven torque produced by a data assimilation which was performed without gravity wave drag. It was shown that the inclusion of gravity wave drag results in large changes in both the mean flow and in eddy fluxes. The result is a more accurate simulation of surface stress (through a reduction in the surface wind strength), of mountain torque (through a redistribution of mean sea-level pressure), and of momentum convergence (through a reduction in the flux of westerly momentum by transient flow eddies).

Boundary Conditions and other Input Data:

Required fields which are not explicitly predicted or diagnosed during model execution must either be prescribed internally or obtained from external data sets. In the fizhi package these fields include: sea surface temperature, sea ice estent, surface geopotential variance, vegetation index, and the radiation-related background levels of: ozone, carbon dioxide, and stratospheric moisture.

Boundary condition data sets are available at the model's resolutions for either climatological or yearly varying conditions. Any frequency of boundary condition data can be used in the fizhi package; however, the current selection of data is summarized in Table 6.15. The time mean values are interpolated during each model timestep to the current time.


Table 6.15: Boundary conditions and other input data used in the fizhi package. Also noted are the current years and frequencies available.
Fizhi Input Datasets


Variable Frequency Years
Sea Ice Extent monthly 1979-current, climatology
Sea Ice Extent weekly 1982-current, climatology
Sea Surface Temperature monthly 1979-current, climatology
Sea Surface Temperature weekly 1982-current, climatology
Zonally Averaged Upper-Level Moisture monthly climatology
Zonally Averaged Ozone Concentration monthly climatology


6.5.3.2.13 Topography and Topography Variance

Surface geopotential heights are provided from an averaging of the Navy 10 minute by 10 minute dataset supplied by the National Center for Atmospheric Research (NCAR) to the model's grid resolution. The original topography is first rotated to the proper grid-orientation which is being run, and then averages the data to the model resolution.

The standard deviation of the subgrid-scale topography is computed by interpolating the 10 minute data to the model's resolution and re-interpolating back to the 10 minute by 10 minute resolution. The sub-grid scale variance is constructed based on this smoothed dataset.

6.5.3.2.14 Upper Level Moisture

The fizhi package uses climatological water vapor data above 100 mb from the Stratospheric Aerosol and Gas Experiment (SAGE) as input into the model's radiation packages. The SAGE data is archived as monthly zonal means at $ 5^\circ$ latitudinal resolution. The data is interpolated to the model's grid location and current time, and blended with the GCM's moisture data. Below 300 mb, the model's moisture data is used. Above 100 mb, the SAGE data is used. Between 100 and 300 mb, a linear interpolation (in pressure) is performed using the data from SAGE and the GCM.

6.5.3.3 Fizhi Diagnostics

Fizhi Diagnostic Menu:

NAME UNITS LEVELS DESCRIPTION
       
UFLUX $ Newton/m^2$ 1
Surface U-Wind Stress on the atmosphere
VFLUX $ Newton/m^2$ 1
Surface V-Wind Stress on the atmosphere
HFLUX $ Watts/m^2$ 1
Surface Flux of Sensible Heat
EFLUX $ Watts/m^2$ 1
Surface Flux of Latent Heat
QICE $ Watts/m^2$ 1
Heat Conduction through Sea-Ice
RADLWG $ Watts/m^2$ 1
Net upward LW flux at the ground
RADSWG $ Watts/m^2$ 1
Net downward SW flux at the ground
RI $ dimensionless$ Nrphys
Richardson Number
CT $ dimensionless$ 1
Surface Drag coefficient for T and Q
CU $ dimensionless$ 1
Surface Drag coefficient for U and V
ET $ m^2/sec$ Nrphys
Diffusivity coefficient for T and Q
EU $ m^2/sec$ Nrphys
Diffusivity coefficient for U and V
TURBU $ m/sec/day$ Nrphys
U-Momentum Changes due to Turbulence
TURBV $ m/sec/day$ Nrphys
V-Momentum Changes due to Turbulence
TURBT $ deg/day$ Nrphys
Temperature Changes due to Turbulence
TURBQ $ g/kg/day$ Nrphys
Specific Humidity Changes due to Turbulence
MOISTT $ deg/day$ Nrphys
Temperature Changes due to Moist Processes
MOISTQ $ g/kg/day$ Nrphys
Specific Humidity Changes due to Moist Processes
RADLW $ deg/day$ Nrphys
Net Longwave heating rate for each level
RADSW $ deg/day$ Nrphys
Net Shortwave heating rate for each level
PREACC $ mm/day$ 1
Total Precipitation
PRECON $ mm/day$ 1
Convective Precipitation
TUFLUX $ Newton/m^2$ Nrphys
Turbulent Flux of U-Momentum
TVFLUX $ Newton/m^2$ Nrphys
Turbulent Flux of V-Momentum
TTFLUX $ Watts/m^2$ Nrphys
Turbulent Flux of Sensible Heat


NAME UNITS LEVELS DESCRIPTION
       
TQFLUX $ Watts/m^2$ Nrphys
Turbulent Flux of Latent Heat
CN $ dimensionless$ 1
Neutral Drag Coefficient
WINDS $ m/sec$ 1
Surface Wind Speed
DTSRF $ deg$ 1
Air/Surface virtual temperature difference
TG $ deg$ 1
Ground temperature
TS $ deg$ 1
Surface air temperature (Adiabatic from lowest model layer)
DTG $ deg$ 1
Ground temperature adjustment
QG $ g/kg$ 1
Ground specific humidity
QS $ g/kg$ 1
Saturation surface specific humidity
TGRLW $ deg$ 1
Instantaneous ground temperature used as input to the Longwave radiation subroutine
ST4 $ Watts/m^2$ 1
Upward Longwave flux at the ground ( $ \sigma T^4$ )
OLR $ Watts/m^2$ 1
Net upward Longwave flux at the top of the model
OLRCLR $ Watts/m^2$ 1
Net upward clearsky Longwave flux at the top of the model
LWGCLR $ Watts/m^2$ 1
Net upward clearsky Longwave flux at the ground
LWCLR $ deg/day$ Nrphys
Net clearsky Longwave heating rate for each level
TLW $ deg$ Nrphys
Instantaneous temperature used as input to the Longwave radiation subroutine
SHLW $ g/g$ Nrphys
Instantaneous specific humidity used as input to the Longwave radiation subroutine
OZLW $ g/g$ Nrphys
Instantaneous ozone used as input to the Longwave radiation subroutine
CLMOLW $ 0-1$ Nrphys
Maximum overlap cloud fraction used in the Longwave radiation subroutine
CLDTOT $ 0-1$ Nrphys
Total cloud fraction used in the Longwave and Shortwave radiation subroutines
LWGDOWN $ Watts/m^2$ 1
Downwelling Longwave radiation at the ground
GWDT $ deg/day$ Nrphys
Temperature tendency due to Gravity Wave Drag
RADSWT $ Watts/m^2$ 1
Incident Shortwave radiation at the top of the atmosphere
TAUCLD $ per 100 mb$ Nrphys
Counted Cloud Optical Depth (non-dimensional) per 100 mb
TAUCLDC $ Number$ Nrphys
Cloud Optical Depth Counter


NAME UNITS LEVELS DESCRIPTION
       
CLDLOW $ 0-1$ Nrphys
Low-Level ( 1000-700 hPa) Cloud Fraction (0-1)
EVAP $ mm/day$ 1
Surface evaporation
DPDT $ hPa/day$ 1
Surface Pressure tendency
UAVE $ m/sec$ Nrphys
Average U-Wind
VAVE $ m/sec$ Nrphys
Average V-Wind
TAVE $ deg$ Nrphys
Average Temperature
QAVE $ g/kg$ Nrphys
Average Specific Humidity
OMEGA $ hPa/day$ Nrphys
Vertical Velocity
DUDT $ m/sec/day$ Nrphys
Total U-Wind tendency
DVDT $ m/sec/day$ Nrphys
Total V-Wind tendency
DTDT $ deg/day$ Nrphys
Total Temperature tendency
DQDT $ g/kg/day$ Nrphys
Total Specific Humidity tendency
VORT $ 10^{-4}/sec$ Nrphys
Relative Vorticity
DTLS $ deg/day$ Nrphys
Temperature tendency due to Stratiform Cloud Formation
DQLS $ g/kg/day$ Nrphys
Specific Humidity tendency due to Stratiform Cloud Formation
USTAR $ m/sec$ 1
Surface USTAR wind
Z0 $ m$ 1
Surface roughness
FRQTRB $ 0-1$ Nrphys-1
Frequency of Turbulence
PBL $ mb$ 1
Planetary Boundary Layer depth
SWCLR $ deg/day$ Nrphys
Net clearsky Shortwave heating rate for each level
OSR $ Watts/m^2$ 1
Net downward Shortwave flux at the top of the model
OSRCLR $ Watts/m^2$ 1
Net downward clearsky Shortwave flux at the top of the model
CLDMAS $ kg / m^2$ Nrphys
Convective cloud mass flux
UAVE $ m/sec$ Nrphys
Time-averaged $ u-Wind$


NAME UNITS LEVELS DESCRIPTION
       
VAVE $ m/sec$ Nrphys
Time-averaged $ v-Wind$
TAVE $ deg$ Nrphys
Time-averaged $ Temperature$
QAVE $ g/g$ Nrphys
Time-averaged $ Specific \, \, Humidity$
RFT $ deg/day$ Nrphys
Temperature tendency due Rayleigh Friction
PS $ mb$ 1
Surface Pressure
QQAVE $ (m/sec)^2$ Nrphys
Time-averaged $ Turbulent Kinetic Energy$
SWGCLR $ Watts/m^2$ 1
Net downward clearsky Shortwave flux at the ground
PAVE $ mb$ 1
Time-averaged Surface Pressure
DIABU $ m/sec/day$ Nrphys
Total Diabatic forcing on $ u-Wind$
DIABV $ m/sec/day$ Nrphys
Total Diabatic forcing on $ v-Wind$
DIABT $ deg/day$ Nrphys
Total Diabatic forcing on $ Temperature$
DIABQ $ g/kg/day$ Nrphys
Total Diabatic forcing on $ Specific \, \, Humidity$
RFU $ m/sec/day$ Nrphys
U-Wind tendency due to Rayleigh Friction
RFV $ m/sec/day$ Nrphys
V-Wind tendency due to Rayleigh Friction
GWDU $ m/sec/day$ Nrphys
U-Wind tendency due to Gravity Wave Drag
GWDU $ m/sec/day$ Nrphys
V-Wind tendency due to Gravity Wave Drag
GWDUS $ N/m^2$ 1
U-Wind Gravity Wave Drag Stress at Surface
GWDVS $ N/m^2$ 1
V-Wind Gravity Wave Drag Stress at Surface
GWDUT $ N/m^2$ 1
U-Wind Gravity Wave Drag Stress at Top
GWDVT $ N/m^2$ 1
V-Wind Gravity Wave Drag Stress at Top
LZRAD $ mg/kg$ Nrphys
Estimated Cloud Liquid Water used in Radiation


NAME UNITS LEVELS DESCRIPTION
       
SLP $ mb$ 1
Time-averaged Sea-level Pressure
CLDFRC $ 0-1$ 1
Total Cloud Fraction
TPW $ gm/cm^2$ 1
Precipitable water
U2M $ m/sec$ 1
U-Wind at 2 meters
V2M $ m/sec$ 1
V-Wind at 2 meters
T2M $ deg$ 1
Temperature at 2 meters
Q2M $ g/kg$ 1
Specific Humidity at 2 meters
U10M $ m/sec$ 1
U-Wind at 10 meters
V10M $ m/sec$ 1
V-Wind at 10 meters
T10M $ deg$ 1
Temperature at 10 meters
Q10M $ g/kg$ 1
Specific Humidity at 10 meters
DTRAIN $ kg / m^2$ Nrphys
Detrainment Cloud Mass Flux
QFILL $ g/kg/day$ Nrphys
Filling of negative specific humidity











NAME UNITS LEVELS DESCRIPTION
       
DTCONV $ deg/sec$ Nr
Temp Change due to Convection
DQCONV $ g/kg/sec$ Nr
Specific Humidity Change due to Convection
RELHUM $ percent$ Nr
Relative Humidity
PRECLS $ g/m^2/sec$ 1
Large Scale Precipitation
ENPREC $ J/g$ 1
Energy of Precipitation (snow, rain Temp)










Fizhi Diagnostic Description:

In this section we list and describe the diagnostic quantities available within the GCM. The diagnostics are listed in the order that they appear in the Diagnostic Menu, Section 6.5.3.3. In all cases, each diagnostic as currently archived on the output datasets is time-averaged over its diagnostic output frequency:

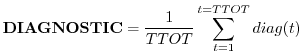
$\displaystyle {\bf DIAGNOSTIC} = \frac{1}{TTOT} \sum_{t=1}^{t=TTOT} diag(t) $

where $ TTOT = \frac{ {\bf NQDIAG} }{\Delta t}$ , NQDIAG is the output frequency of the diagnostic, and $ \Delta t$ is the timestep over which the diagnostic is updated.

UFLUX Surface Zonal Wind Stress on the Atmosphere ( $ Newton/m^2$ )

The zonal wind stress is the turbulent flux of zonal momentum from the surface.

$\displaystyle {\bf UFLUX} = - \rho C_D W_s u \hspace{1cm}where: \hspace{.2cm}C_D = C^2_u $

where $ \rho $ = the atmospheric density at the surface, $ C_{D}$ is the surface drag coefficient, $ C_u$ is the dimensionless surface exchange coefficient for momentum (see diagnostic number 10), $ W_s$ is the magnitude of the surface layer wind, and $ u$ is the zonal wind in the lowest model layer.

VFLUX Surface Meridional Wind Stress on the Atmosphere ( $ Newton/m^2$ )

The meridional wind stress is the turbulent flux of meridional momentum from the surface.

$\displaystyle {\bf VFLUX} = - \rho C_D W_s v \hspace{1cm}where: \hspace{.2cm}C_D = C^2_u $

where $ \rho $ = the atmospheric density at the surface, $ C_{D}$ is the surface drag coefficient, $ C_u$ is the dimensionless surface exchange coefficient for momentum (see diagnostic number 10), $ W_s$ is the magnitude of the surface layer wind, and $ v$ is the meridional wind in the lowest model layer.

HFLUX Surface Flux of Sensible Heat ($ Watts/m^2$ )

The turbulent flux of sensible heat from the surface to the atmosphere is a function of the gradient of virtual potential temperature and the eddy exchange coefficient:

$\displaystyle {\bf HFLUX} = P^{\kappa}\rho c_{p} C_{H} W_s (\theta_{surface} - \theta_{Nrphys}) \hspace{1cm}where: \hspace{.2cm}C_H = C_u C_t $

where $ \rho $ = the atmospheric density at the surface, $ c_{p}$ is the specific heat of air, $ C_{H}$ is the dimensionless surface heat transfer coefficient, $ W_s$ is the magnitude of the surface layer wind, $ C_u$ is the dimensionless surface exchange coefficient for momentum (see diagnostic number 10), $ C_t$ is the dimensionless surface exchange coefficient for heat and moisture (see diagnostic number 9), and $ \theta $ is the potential temperature at the surface and at the bottom model level.

EFLUX Surface Flux of Latent Heat ($ Watts/m^2$ )

The turbulent flux of latent heat from the surface to the atmosphere is a function of the gradient of moisture, the potential evapotranspiration fraction and the eddy exchange coefficient:

$\displaystyle {\bf EFLUX} = \rho \beta L C_{H} W_s (q_{surface} - q_{Nrphys}) \hspace{1cm}where: \hspace{.2cm}C_H = C_u C_t $

where $ \rho $ = the atmospheric density at the surface, $ \beta$ is the fraction of the potential evapotranspiration actually evaporated, L is the latent heat of evaporation, $ C_{H}$ is the dimensionless surface heat transfer coefficient, $ W_s$ is the magnitude of the surface layer wind, $ C_u$ is the dimensionless surface exchange coefficient for momentum (see diagnostic number 10), $ C_t$ is the dimensionless surface exchange coefficient for heat and moisture (see diagnostic number 9), and $ q_{surface}$ and $ q_{Nrphys}$ are the specific humidity at the surface and at the bottom model level, respectively.

QICE Heat Conduction Through Sea Ice ($ Watts/m^2$ )

Over sea ice there is an additional source of energy at the surface due to the heat conduction from the relatively warm ocean through the sea ice. The heat conduction through sea ice represents an additional energy source term for the ground temperature equation.

$\displaystyle {\bf QICE} = \frac{C_{ti}}{H_i} (T_i-T_g) $

where $ C_{ti}$ is the thermal conductivity of ice, $ H_i$ is the ice thickness, assumed to be $ 3 \hspace{.1cm} m$ where sea ice is present, $ T_i$ is 273 degrees Kelvin, and $ T_g$ is the temperature of the sea ice.

NOTE: QICE is not available through model version 5.3, but is available in subsequent versions.

RADLWG Net upward Longwave Flux at the surface ($ Watts/m^2$ )


$\displaystyle {\bf RADLWG}$ $\displaystyle =$ $\displaystyle F_{LW,Nrphys+1}^{Net}$  
  $\displaystyle =$ $\displaystyle F_{LW,Nrphys+1}^\uparrow - F_{LW,Nrphys+1}^\downarrow$  


where Nrphys+1 indicates the lowest model edge-level, or $ p = p_{surf}$ . $ F_{LW}^\uparrow$ is the upward Longwave flux and $ F_{LW}^\downarrow$ is the downward Longwave flux.

RADSWG Net downard shortwave Flux at the surface ($ Watts/m^2$ )


$\displaystyle {\bf RADSWG}$ $\displaystyle =$ $\displaystyle F_{SW,Nrphys+1}^{Net}$  
  $\displaystyle =$ $\displaystyle F_{SW,Nrphys+1}^\downarrow - F_{SW,Nrphys+1}^\uparrow$  


where Nrphys+1 indicates the lowest model edge-level, or $ p = p_{surf}$ . $ F_{SW}^\downarrow$ is the downward Shortwave flux and $ F_{SW}^\uparrow$ is the upward Shortwave flux.

RI Richardson Number ( $ dimensionless$ )

The non-dimensional stability indicator is the ratio of the buoyancy to the shear:

$\displaystyle {\bf RI} = \frac{ \frac{g}{\theta_v} \frac{\partial \theta_v}{\pa... ... z} }{ (\frac{\partial u}{\partial z})^2 + (\frac{\partial v}{\partial z})^2 } $


where we used the hydrostatic equation:

$\displaystyle {\frac{\partial \Phi}{\partial P^ \kappa}} = c_p \theta_v $

Negative values indicate unstable buoyancy AND shear, small positive values ($ <0.4$ ) indicate dominantly unstable shear, and large positive values indicate dominantly stable stratification.

CT Surface Exchange Coefficient for Temperature and Moisture ( $ dimensionless$ )

The surface exchange coefficient is obtained from the similarity functions for the stability dependant flux profile relationships:

$\displaystyle {\bf CT} = -\frac{( \overline{w^{\prime}\theta^{\prime}} ) }{ u_*... ...\prime}q^{\prime}} ) }{ u_* \Delta q } = \frac{ k }{ (\psi_{h} + \psi_{g}) } $

where $ \psi_h$ is the surface layer non-dimensional temperature change and $ \psi_g$ is the viscous sublayer non-dimensional temperature or moisture change:

$\displaystyle \psi_{h} = \int_{\zeta_{0}}^{\zeta} \frac{\phi_{h} }{ \zeta} d \z... ...5 (Pr^{2/3} - 0.2) }{ \nu^{1/2} } (h_{0}u_{*} - h_{0_{ref}}u_{*_{ref}})^{1/2} $

and: $ h_{0} = 30z_{0}$ with a maximum value over land of 0.01

$ \phi_h$ is the similarity function of $ \zeta$ , which expresses the stability dependance of the temperature and moisture gradients, specified differently for stable and unstable layers according to Helfand and Schubert [1995]. k is the Von Karman constant, $ \zeta$ is the non-dimensional stability parameter, Pr is the Prandtl number for air, $ \nu$ is the molecular viscosity, $ z_{0}$ is the surface roughness length, $ u_*$ is the surface stress velocity (see diagnostic number 67), and the subscript ref refers to a reference value.

CU Surface Exchange Coefficient for Momentum ( $ dimensionless$ )

The surface exchange coefficient is obtained from the similarity functions for the stability dependant flux profile relationships:

$\displaystyle {\bf CU} = \frac{u_* }{ W_s} = \frac{ k }{ \psi_{m} } $

where $ \psi_m$ is the surface layer non-dimensional wind shear:

$\displaystyle \psi_{m} = {\int_{\zeta_{0}}^{\zeta} \frac{\phi_{m} }{ \zeta} d \zeta} $

$ \phi_m$ is the similarity function of $ \zeta$ , which expresses the stability dependance of the temperature and moisture gradients, specified differently for stable and unstable layers according to Helfand and Schubert [1995]. k is the Von Karman constant, $ \zeta$ is the non-dimensional stability parameter, $ u_*$ is the surface stress velocity (see diagnostic number 67), and $ W_s$ is the magnitude of the surface layer wind.

ET Diffusivity Coefficient for Temperature and Moisture ($ m^2/sec$ )

In the level 2.5 version of the Mellor-Yamada (1974) hierarchy, the turbulent heat or moisture flux for the atmosphere above the surface layer can be expressed as a turbulent diffusion coefficient $ K_h$ times the negative of the gradient of potential temperature or moisture. In the Helfand and Labraga [1988] adaptation of this closure, $ K_h$ takes the form:

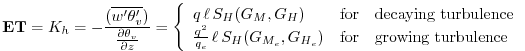
$\displaystyle {\bf ET} = K_h = -\frac{( \overline{w^{\prime}\theta_v^{\prime}})... ...\ell \, S_{H}(G_{M_e},G_{H_e}) & \mbox{growing turbulence} \end{array} \right. $

where $ q$ is the turbulent velocity, or $ \sqrt{2*turbulent \hspace{.2cm} kinetic \hspace{.2cm} energy}$ , $ q_e$ is the turbulence velocity derived from the more simple level 2.0 model, which describes equilibrium turbulence, $ \ell$ is the master length scale related to the layer depth, $ S_H$ is a function of $ G_H$ and $ G_M$ , the dimensionless buoyancy and wind shear parameters, respectively, or a function of $ G_{H_e}$ and $ G_{M_e}$ , the equilibrium dimensionless buoyancy and wind shear parameters. Both $ G_H$ and $ G_M$ , and their equilibrium values $ G_{H_e}$ and $ G_{M_e}$ , are functions of the Richardson number.

For the detailed equations and derivations of the modified level 2.5 closure scheme, see Helfand and Labraga [1988].

In the surface layer, $ {\bf {ET}}$ is the exchange coefficient for heat and moisture, in units of $ m/sec$ , given by:

$\displaystyle {\bf ET_{Nrphys}} = C_t * u_* = C_H W_s $

where $ C_t$ is the dimensionless exchange coefficient for heat and moisture from the surface layer similarity functions (see diagnostic number 9), $ u_*$ is the surface friction velocity (see diagnostic number 67), $ C_H$ is the heat transfer coefficient, and $ W_s$ is the magnitude of the surface layer wind.

EU Diffusivity Coefficient for Momentum ($ m^2/sec$ )

In the level 2.5 version of the Mellor-Yamada (1974) hierarchy, the turbulent heat momentum flux for the atmosphere above the surface layer can be expressed as a turbulent diffusion coefficient $ K_m$ times the negative of the gradient of the u-wind. In the Helfand and Labraga [1988] adaptation of this closure, $ K_m$ takes the form:

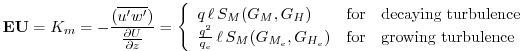
$\displaystyle {\bf EU} = K_m = -\frac{( \overline{u^{\prime}w^{\prime}} ) }{ \f... ...\ell \, S_{M}(G_{M_e},G_{H_e}) & \mbox{growing turbulence} \end{array} \right. $

where $ q$ is the turbulent velocity, or $ \sqrt{2*turbulent \hspace{.2cm} kinetic \hspace{.2cm} energy}$ , $ q_e$ is the turbulence velocity derived from the more simple level 2.0 model, which describes equilibrium turbulence, $ \ell$ is the master length scale related to the layer depth, $ S_M$ is a function of $ G_H$ and $ G_M$ , the dimensionless buoyancy and wind shear parameters, respectively, or a function of $ G_{H_e}$ and $ G_{M_e}$ , the equilibrium dimensionless buoyancy and wind shear parameters. Both $ G_H$ and $ G_M$ , and their equilibrium values $ G_{H_e}$ and $ G_{M_e}$ , are functions of the Richardson number.

For the detailed equations and derivations of the modified level 2.5 closure scheme, see Helfand and Labraga [1988].

In the surface layer, $ {\bf {EU}}$ is the exchange coefficient for momentum, in units of $ m/sec$ , given by:

$\displaystyle {\bf EU_{Nrphys}} = C_u * u_* = C_D W_s $

where $ C_u$ is the dimensionless exchange coefficient for momentum from the surface layer similarity functions (see diagnostic number 10), $ u_*$ is the surface friction velocity (see diagnostic number 67), $ C_D$ is the surface drag coefficient, and $ W_s$ is the magnitude of the surface layer wind.

TURBU Zonal U-Momentum changes due to Turbulence ($ m/sec/day$ )

The tendency of U-Momentum due to turbulence is written:

$\displaystyle {\bf TURBU} = {\frac{\partial u}{\partial t}}_{turb} = {\frac{\pa... ...me}})} = {\frac{\partial }{\partial z} }{(K_m \frac{\partial u}{\partial z})} $

The Helfand and Labraga level 2.5 scheme models the turbulent flux of u-momentum in terms of $ K_m$ , and the equation has the form of a diffusion equation.

TURBV Meridional V-Momentum changes due to Turbulence ($ m/sec/day$ )

The tendency of V-Momentum due to turbulence is written:

$\displaystyle {\bf TURBV} = {\frac{\partial v}{\partial t}}_{turb} = {\frac{\pa... ...me}})} = {\frac{\partial }{\partial z} }{(K_m \frac{\partial v}{\partial z})} $

The Helfand and Labraga level 2.5 scheme models the turbulent flux of v-momentum in terms of $ K_m$ , and the equation has the form of a diffusion equation.

TURBT Temperature changes due to Turbulence ($ deg/day$ )

The tendency of temperature due to turbulence is written:

$\displaystyle {\bf TURBT} = {\frac{\partial T}{\partial t}} = P^{\kappa}{\frac{... ...pa}{\frac{\partial }{\partial z} }{(K_h \frac{\partial \theta_v}{\partial z})} $

The Helfand and Labraga level 2.5 scheme models the turbulent flux of temperature in terms of $ K_h$ , and the equation has the form of a diffusion equation.

TURBQ Specific Humidity changes due to Turbulence ($ g/kg/day$ )

The tendency of specific humidity due to turbulence is written:

$\displaystyle {\bf TURBQ} = {\frac{\partial q}{\partial t}}_{turb} = {\frac{\pa... ...me}})} = {\frac{\partial }{\partial z} }{(K_h \frac{\partial q}{\partial z})} $

The Helfand and Labraga level 2.5 scheme models the turbulent flux of temperature in terms of $ K_h$ , and the equation has the form of a diffusion equation.

MOISTT Temperature Changes Due to Moist Processes ($ deg/day$ )

$\displaystyle {\bf MOISTT} = \left. {\frac{\partial T}{\partial t}}\right\vert _{c} + \left. {\frac{\partial T}{\partial t}} \right\vert _{ls} $

where:

$\displaystyle \left.{\frac{\partial T}{\partial t}}\right\vert _{c} = R \sum_i ... ...\left.{\frac{\partial T}{\partial t}}\right\vert _{ls} = \frac{L}{c_p} (q^*-q) $

and

$\displaystyle \Gamma_s = g \eta \frac{\partial s}{\partial p} $

The subscript $ c$ refers to convective processes, while the subscript $ ls$ refers to large scale precipitation processes, or supersaturation rain. The summation refers to contributions from each cloud type called by RAS. The dry static energy is given as $ s$ , the convective cloud base mass flux is given as $ m_B$ , and the cloud entrainment is given as $ \eta $ , which are explicitly defined in Section 6.5.3.2, the description of the convective parameterization. The fractional adjustment, or relaxation parameter, for each cloud type is given as $ \alpha $ , while $ R$ is the rain re-evaporation adjustment.

MOISTQ Specific Humidity Changes Due to Moist Processes ($ g/kg/day$ )

$\displaystyle {\bf MOISTQ} = \left. {\frac{\partial q}{\partial t}}\right\vert _{c} + \left. {\frac{\partial q}{\partial t}} \right\vert _{ls} $

where:

$\displaystyle \left.{\frac{\partial q}{\partial t}}\right\vert _{c} = R \sum_i ... ...\hspace{.4cm} \left.{\frac{\partial q}{\partial t}}\right\vert _{ls} = (q^*-q) $

and

$\displaystyle \Gamma_s = g \eta \frac{\partial s}{\partial p}\hspace{.4cm} and \hspace{.4cm}\Gamma_h = g \eta \frac{\partial h}{\partial p} $

The subscript $ c$ refers to convective processes, while the subscript $ ls$ refers to large scale precipitation processes, or supersaturation rain. The summation refers to contributions from each cloud type called by RAS. The dry static energy is given as $ s$ , the moist static energy is given as $ h$ , the convective cloud base mass flux is given as $ m_B$ , and the cloud entrainment is given as $ \eta $ , which are explicitly defined in Section 6.5.3.2, the description of the convective parameterization. The fractional adjustment, or relaxation parameter, for each cloud type is given as $ \alpha $ , while $ R$ is the rain re-evaporation adjustment.

RADLW Heating Rate due to Longwave Radiation ($ deg/day$ )

The net longwave heating rate is calculated as the vertical divergence of the net terrestrial radiative fluxes. Both the clear-sky and cloudy-sky longwave fluxes are computed within the longwave routine. The subroutine calculates the clear-sky flux, $ F^{clearsky}_{LW}$ , first. For a given cloud fraction, the clear line-of-sight probability $ C(p,p^{\prime})$ is computed from the current level pressure $ p$ to the model top pressure, $ p^{\prime} = p_{top}$ , and the model surface pressure, $ p^{\prime} = p_{surf}$ , for the upward and downward radiative fluxes. (see Section 6.5.3.2). The cloudy-sky flux is then obtained as:

$\displaystyle F_{LW} = C(p,p') \cdot F^{clearsky}_{LW}, $

Finally, the net longwave heating rate is calculated as the vertical divergence of the net terrestrial radiative fluxes:

$\displaystyle \frac{\partial \rho c_p T}{\partial t} = - \frac{\partial }{\partial z} F_{LW}^{NET} , $

or

$\displaystyle {\bf RADLW} = \frac{g}{c_p \pi} \frac{\partial }{\partial \sigma} F_{LW}^{NET} . $

where $ g$ is the accelation due to gravity, $ c_p$ is the heat capacity of air at constant pressure, and

$\displaystyle F_{LW}^{NET} = F_{LW}^\uparrow - F_{LW}^\downarrow $


RADSW Heating Rate due to Shortwave Radiation ($ deg/day$ )

The net Shortwave heating rate is calculated as the vertical divergence of the net solar radiative fluxes. The clear-sky and cloudy-sky shortwave fluxes are calculated separately. For the clear-sky case, the shortwave fluxes and heating rates are computed with both CLMO (maximum overlap cloud fraction) and CLRO (random overlap cloud fraction) set to zero (see Section 6.5.3.2). The shortwave routine is then called a second time, for the cloudy-sky case, with the true time-averaged cloud fractions CLMO and CLRO being used. In all cases, a normalized incident shortwave flux is used as input at the top of the atmosphere.

The heating rate due to Shortwave Radiation under cloudy skies is defined as:

$\displaystyle \frac{\partial \rho c_p T}{\partial t} = - \frac{\partial }{\partial z} F(cloudy)_{SW}^{NET} \cdot {\rm RADSWT}, $

or

$\displaystyle {\bf RADSW} = \frac{g}{c_p \pi} \frac{\partial }{\partial \sigma} F(cloudy)_{SW}^{NET}\cdot {\rm RADSWT} . $

where $ g$ is the accelation due to gravity, $ c_p$ is the heat capacity of air at constant pressure, RADSWT is the true incident shortwave radiation at the top of the atmosphere (See Diagnostic #48), and

$\displaystyle F(cloudy)_{SW}^{Net} = F(cloudy)_{SW}^\uparrow - F(cloudy)_{SW}^\downarrow $


PREACC Total (Large-scale + Convective) Accumulated Precipition ($ mm/day$ )

For a change in specific humidity due to moist processes, $ \Delta q_{moist}$ , the vertical integral or total precipitable amount is given by:

$\displaystyle {\bf PREACC} = \int_{surf}^{top} \rho \Delta q_{moist} dz = - \in... ...{top} \Delta q_{moist} \frac{dp}{g} = \frac{1}{g} \int_0^1 \Delta q_{moist} dp $


A precipitation rate is defined as the vertically integrated moisture adjustment per Moist Processes time step, scaled to $ mm/day$ .

PRECON Convective Precipition ($ mm/day$ )

For a change in specific humidity due to sub-grid scale cumulus convective processes, $ \Delta q_{cum}$ , the vertical integral or total precipitable amount is given by:

$\displaystyle {\bf PRECON} = \int_{surf}^{top} \rho \Delta q_{cum} dz = - \int_{surf}^{top} \Delta q_{cum} \frac{dp}{g} = \frac{1}{g} \int_0^1 \Delta q_{cum} dp $


A precipitation rate is defined as the vertically integrated moisture adjustment per Moist Processes time step, scaled to $ mm/day$ .

TUFLUX Turbulent Flux of U-Momentum ( $ Newton/m^2$ )

The turbulent flux of u-momentum is calculated for $ diagnostic \hspace{.2cm} purposes \hspace{.2cm} only$ from the eddy coefficient for momentum:

$\displaystyle {\bf TUFLUX} = {\rho } {(\overline{u^{\prime}w^{\prime}})} = {\rho } {(- K_m \frac{\partial U}{\partial z})} $

where $ \rho $ is the air density, and $ K_m$ is the eddy coefficient.

TVFLUX Turbulent Flux of V-Momentum ( $ Newton/m^2$ )

The turbulent flux of v-momentum is calculated for $ diagnostic \hspace{.2cm} purposes \hspace{.2cm} only$ from the eddy coefficient for momentum:

$\displaystyle {\bf TVFLUX} = {\rho } {(\overline{v^{\prime}w^{\prime}})} = {\rho } {(- K_m \frac{\partial V}{\partial z})} $

where $ \rho $ is the air density, and $ K_m$ is the eddy coefficient.

TTFLUX Turbulent Flux of Sensible Heat ($ Watts/m^2$ )

The turbulent flux of sensible heat is calculated for $ diagnostic \hspace{.2cm} purposes \hspace{.2cm} only$ from the eddy coefficient for heat and moisture:

$\displaystyle {\bf TTFLUX} = c_p {\rho } P^{\kappa}{(\overline{w^{\prime}\thet... ...me}})} = c_p {\rho } P^{\kappa}{(- K_h \frac{\partial \theta_v}{\partial z})} $

where $ \rho $ is the air density, and $ K_h$ is the eddy coefficient.

TQFLUX Turbulent Flux of Latent Heat ($ Watts/m^2$ )

The turbulent flux of latent heat is calculated for $ diagnostic \hspace{.2cm} purposes \hspace{.2cm} only$ from the eddy coefficient for heat and moisture:

$\displaystyle {\bf TQFLUX} = {L {\rho } (\overline{w^{\prime}q^{\prime}})} = {L {\rho }(- K_h \frac{\partial q}{\partial z})} $

where $ \rho $ is the air density, and $ K_h$ is the eddy coefficient.

CN Neutral Drag Coefficient ( $ dimensionless$ )

The drag coefficient for momentum obtained by assuming a neutrally stable surface layer:

$\displaystyle {\bf CN} = \frac{ k }{ \ln(\frac{h }{z_0}) } $

where $ k$ is the Von Karman constant, $ h$ is the height of the surface layer, and $ z_0$ is the surface roughness.

NOTE: CN is not available through model version 5.3, but is available in subsequent versions.

WINDS Surface Wind Speed ($ meter/sec$ )

The surface wind speed is calculated for the last internal turbulence time step:

$\displaystyle {\bf WINDS} = \sqrt{u_{Nrphys}^2 + v_{Nrphys}^2} $

where the subscript $ Nrphys$ refers to the lowest model level.

DTSRF Air/Surface Virtual Temperature Difference ( $ deg \hspace{.1cm} K$ )

The air/surface virtual temperature difference measures the stability of the surface layer:

$\displaystyle {\bf DTSRF} = (\theta_{v{Nrphys+1}} - \theta{v_{Nrphys}}) P^{\kappa}_{surf} $

where

$\displaystyle \theta_{v{Nrphys+1}} = \frac{ T_g }{ P^{\kappa}_{surf} } (1 + .60... ... and \hspace{1cm} q_{Nrphys+1} = q_{Nrphys} + \beta(q^*(T_g,P_s) - q_{Nrphys}) $

$ \beta$ is the surface potential evapotranspiration coefficient ($ \beta=1$ over oceans), $ q^*(T_g,P_s)$ is the saturation specific humidity at the ground temperature and surface pressure, level $ Nrphys$ refers to the lowest model level and level $ Nrphys+1$ refers to the surface.

TG Ground Temperature ( $ deg \hspace{.1cm} K$ )

The ground temperature equation is solved as part of the turbulence package using a backward implicit time differencing scheme:

$\displaystyle {\bf TG} \hspace{.1cm} is \hspace{.1cm} obtained \hspace{.1cm} fr... ...{.1cm} C_g\frac{\partial T_g}{\partial t} = R_{sw} - R_{lw} + Q_{ice} - H - LE $

where $ R_{sw}$ is the net surface downward shortwave radiative flux, $ R_{lw}$ is the net surface upward longwave radiative flux, $ Q_{ice}$ is the heat conduction through sea ice, $ H$ is the upward sensible heat flux, $ LE$ is the upward latent heat flux, and $ C_g$ is the total heat capacity of the ground. $ C_g$ is obtained by solving a heat diffusion equation for the penetration of the diurnal cycle into the ground (Blackadar [1977]), and is given by:

$\displaystyle C_g = \sqrt{ \frac{\lambda C_s }{ 2 \omega } } = \sqrt{(0.386 + 0.536W + 0.15W^2)2x10^{-3} \frac{86400.}{2\pi} } \, \, . $

Here, the thermal conductivity, $ \lambda $ , is equal to $ 2x10^{-3}$ $ \frac{ly}{sec} \frac{cm}{K}$ , the angular velocity of the earth, $ \omega$ , is written as $ 86400$ $ sec/day$ divided by $ 2 \pi$ $ radians/ day$ , and the expression for $ C_s$ , the heat capacity per unit volume at the surface, is a function of the ground wetness, $ W$ .

TS Surface Temperature ( $ deg \hspace{.1cm} K$ )

The surface temperature estimate is made by assuming that the model's lowest layer is well-mixed, and therefore that $ \theta $ is constant in that layer. The surface temperature is therefore:

$\displaystyle {\bf TS} = \theta_{Nrphys} P^{\kappa}_{surf} $


DTG Surface Temperature Adjustment ( $ deg \hspace{.1cm} K$ )

The change in surface temperature from one turbulence time step to the next, solved using the Ground Temperature Equation (see diagnostic number 30) is calculated:

$\displaystyle {\bf DTG} = {T_g}^{n} - {T_g}^{n-1} $

where superscript $ n$ refers to the new, updated time level, and the superscript $ n-1$ refers to the value at the previous turbulence time level.

QG Ground Specific Humidity ($ g/kg$ )

The ground specific humidity is obtained by interpolating between the specific humidity at the lowest model level and the specific humidity of a saturated ground. The interpolation is performed using the potential evapotranspiration function:

$\displaystyle {\bf QG} = q_{Nrphys+1} = q_{Nrphys} + \beta(q^*(T_g,P_s) - q_{Nrphys}) $

where $ \beta$ is the surface potential evapotranspiration coefficient ($ \beta=1$ over oceans), and $ q^*(T_g,P_s)$ is the saturation specific humidity at the ground temperature and surface pressure.

QS Saturation Surface Specific Humidity ($ g/kg$ )

The surface saturation specific humidity is the saturation specific humidity at the ground temprature and surface pressure:

$\displaystyle {\bf QS} = q^*(T_g,P_s) $


TGRLW Instantaneous ground temperature used as input to the Longwave radiation subroutine (deg)

$\displaystyle {\bf TGRLW} = T_g(\lambda , \phi ,n) $

where $ T_g$ is the model ground temperature at the current time step $ n$ .

ST4 Upward Longwave flux at the surface ($ Watts/m^2$ )

$\displaystyle {\bf ST4} = \sigma T^4 $

where $ \sigma $ is the Stefan-Boltzmann constant and T is the temperature.

OLR Net upward Longwave flux at $ p=p_{top}$ ($ Watts/m^2$ )

$\displaystyle {\bf OLR} = F_{LW,top}^{NET} $

where top indicates the top of the first model layer. In the GCM, $ p_{top}$ = 0.0 mb.

OLRCLR Net upward clearsky Longwave flux at $ p=p_{top}$ ($ Watts/m^2$ )

$\displaystyle {\bf OLRCLR} = F(clearsky)_{LW,top}^{NET} $

where top indicates the top of the first model layer. In the GCM, $ p_{top}$ = 0.0 mb.

LWGCLR Net upward clearsky Longwave flux at the surface ($ Watts/m^2$ )


$\displaystyle {\bf LWGCLR}$ $\displaystyle =$ $\displaystyle F(clearsky)_{LW,Nrphys+1}^{Net}$  
  $\displaystyle =$ $\displaystyle F(clearsky)_{LW,Nrphys+1}^\uparrow - F(clearsky)_{LW,Nrphys+1}^\downarrow$  

where Nrphys+1 indicates the lowest model edge-level, or $ p = p_{surf}$ . $ F(clearsky)_{LW}^\uparrow$ is the upward clearsky Longwave flux and the $ F(clearsky)_{LW}^\downarrow$ is the downward clearsky Longwave flux.

LWCLR Heating Rate due to Clearsky Longwave Radiation ($ deg/day$ )

The net longwave heating rate is calculated as the vertical divergence of the net terrestrial radiative fluxes. Both the clear-sky and cloudy-sky longwave fluxes are computed within the longwave routine. The subroutine calculates the clear-sky flux, $ F^{clearsky}_{LW}$ , first. For a given cloud fraction, the clear line-of-sight probability $ C(p,p^{\prime})$ is computed from the current level pressure $ p$ to the model top pressure, $ p^{\prime} = p_{top}$ , and the model surface pressure, $ p^{\prime} = p_{surf}$ , for the upward and downward radiative fluxes. (see Section 6.5.3.2). The cloudy-sky flux is then obtained as:

$\displaystyle F_{LW} = C(p,p') \cdot F^{clearsky}_{LW}, $

Thus, LWCLR is defined as the net longwave heating rate due to the vertical divergence of the clear-sky longwave radiative flux:

$\displaystyle \frac{\partial \rho c_p T}{\partial t}_{clearsky} = - \frac{\partial }{\partial z} F(clearsky)_{LW}^{NET} , $

or

$\displaystyle {\bf LWCLR} = \frac{g}{c_p \pi} \frac{\partial }{\partial \sigma} F(clearsky)_{LW}^{NET} . $

where $ g$ is the accelation due to gravity, $ c_p$ is the heat capacity of air at constant pressure, and

$\displaystyle F(clearsky)_{LW}^{Net} = F(clearsky)_{LW}^\uparrow - F(clearsky)_{LW}^\downarrow $


TLW Instantaneous temperature used as input to the Longwave radiation subroutine (deg)

$\displaystyle {\bf TLW} = T(\lambda , \phi ,level, n) $

where $ T$ is the model temperature at the current time step $ n$ .

SHLW Instantaneous specific humidity used as input to the Longwave radiation subroutine (kg/kg)

$\displaystyle {\bf SHLW} = q(\lambda , \phi , level , n) $

where $ q$ is the model specific humidity at the current time step $ n$ .

OZLW Instantaneous ozone used as input to the Longwave radiation subroutine (kg/kg)

$\displaystyle {\bf OZLW} = {\rm OZ}(\lambda , \phi , level , n) $

where $ \rm OZ$ is the interpolated ozone data set from the climatological monthly mean zonally averaged ozone data set.

CLMOLW Maximum Overlap cloud fraction used in LW Radiation ($ 0-1$ )

CLMOLW is the time-averaged maximum overlap cloud fraction that has been filled by the Relaxed Arakawa/Schubert Convection scheme and will be used in the Longwave Radiation algorithm. These are convective clouds whose radiative characteristics are assumed to be correlated in the vertical. For a complete description of cloud/radiative interactions, see Section 6.5.3.2.

$\displaystyle {\bf CLMOLW} = CLMO_{RAS,LW}(\lambda, \phi, level ) $


CLDTOT Total cloud fraction used in LW and SW Radiation ($ 0-1$ )

CLDTOT is the time-averaged total cloud fraction that has been filled by the Relaxed Arakawa/Schubert and Large-scale Convection schemes and will be used in the Longwave and Shortwave Radiation packages. For a complete description of cloud/radiative interactions, see Section 6.5.3.2.

$\displaystyle {\bf CLDTOT} = F_{RAS} + F_{LS} $


where $ F_{RAS}$ is the time-averaged cloud fraction due to sub-grid scale convection, and $ F_{LS}$ is the time-averaged cloud fraction due to precipitating and non-precipitating large-scale moist processes.

CLMOSW Maximum Overlap cloud fraction used in SW Radiation ($ 0-1$ )

CLMOSW is the time-averaged maximum overlap cloud fraction that has been filled by the Relaxed Arakawa/Schubert Convection scheme and will be used in the Shortwave Radiation algorithm. These are convective clouds whose radiative characteristics are assumed to be correlated in the vertical. For a complete description of cloud/radiative interactions, see Section 6.5.3.2.

$\displaystyle {\bf CLMOSW} = CLMO_{RAS,SW}(\lambda, \phi, level ) $


CLROSW Random Overlap cloud fraction used in SW Radiation ($ 0-1$ )

CLROSW is the time-averaged random overlap cloud fraction that has been filled by the Relaxed Arakawa/Schubert and Large-scale Convection schemes and will be used in the Shortwave Radiation algorithm. These are convective and large-scale clouds whose radiative characteristics are not assumed to be correlated in the vertical. For a complete description of cloud/radiative interactions, see Section 6.5.3.2.

$\displaystyle {\bf CLROSW} = CLRO_{RAS,Large Scale,SW}(\lambda, \phi, level ) $


RADSWT Incident Shortwave radiation at the top of the atmosphere ($ Watts/m^2$ )

$\displaystyle {\bf RADSWT} = {\frac{S_0}{R_a^2}} \cdot cos \phi_z $

where $ S_0$ , is the extra-terrestial solar contant, $ R_a$ is the earth-sun distance in Astronomical Units, and $ cos \phi_z$ is the cosine of the zenith angle. It should be noted that RADSWT, as well as OSR and OSRCLR, are calculated at the top of the atmosphere (p=0 mb). However, the OLR and OLRCLR diagnostics are currently calculated at $ p=p_{top}$ (0.0 mb for the GCM).

EVAP Surface Evaporation ($ mm/day$ )

The surface evaporation is a function of the gradient of moisture, the potential evapotranspiration fraction and the eddy exchange coefficient:

$\displaystyle {\bf EVAP} = \rho \beta K_{h} (q_{surface} - q_{Nrphys}) $

where $ \rho $ = the atmospheric density at the surface, $ \beta$ is the fraction of the potential evapotranspiration actually evaporated ($ \beta=1$ over oceans), $ K_{h}\ $ is the turbulent eddy exchange coefficient for heat and moisture at the surface in $ m/sec$ and $ q{surface}$ and $ q_{Nrphys}$ are the specific humidity at the surface (see diagnostic number 34) and at the bottom model level, respectively.

DUDT Total Zonal U-Wind Tendency ($ m/sec/day$ )

DUDT is the total time-tendency of the Zonal U-Wind due to Hydrodynamic, Diabatic, and Analysis forcing.

$\displaystyle {\bf DUDT} = \frac{\partial u}{\partial t}_{Dynamics} + \frac{\pa... ...artial u}{\partial t}_{Turbulence} + \frac{\partial u}{\partial t}_{Analysis} $


DVDT Total Zonal V-Wind Tendency ($ m/sec/day$ )

DVDT is the total time-tendency of the Meridional V-Wind due to Hydrodynamic, Diabatic, and Analysis forcing.

$\displaystyle {\bf DVDT} = \frac{\partial v}{\partial t}_{Dynamics} + \frac{\pa... ...artial v}{\partial t}_{Turbulence} + \frac{\partial v}{\partial t}_{Analysis} $


DTDT Total Temperature Tendency ($ deg/day$ )

DTDT is the total time-tendency of Temperature due to Hydrodynamic, Diabatic, and Analysis forcing.

$\displaystyle {\bf DTDT}$ $\displaystyle =$ $\displaystyle \frac{\partial T}{\partial t}_{Dynamics} + \frac{\partial T}{\partial t}_{Moist Processes} + \frac{\partial T}{\partial t}_{Shortwave Radiation}$  
  $\displaystyle +$ $\displaystyle \frac{\partial T}{\partial t}_{Longwave Radiation} + \frac{\partial T}{\partial t}_{Turbulence} + \frac{\partial T}{\partial t}_{Analysis}$  


DQDT Total Specific Humidity Tendency ($ g/kg/day$ )

DQDT is the total time-tendency of Specific Humidity due to Hydrodynamic, Diabatic, and Analysis forcing.

$\displaystyle {\bf DQDT} = \frac{\partial q}{\partial t}_{Dynamics} + \frac{\pa... ...artial q}{\partial t}_{Turbulence} + \frac{\partial q}{\partial t}_{Analysis} $


USTAR Surface-Stress Velocity ($ m/sec$ )

The surface stress velocity, or the friction velocity, is the wind speed at the surface layer top impeded by the surface drag:

$\displaystyle {\bf USTAR} = C_uW_s \hspace{1cm}where: \hspace{.2cm} C_u = \frac{k}{\psi_m} $

$ C_u$ is the non-dimensional surface drag coefficient (see diagnostic number 10), and $ W_s$ is the surface wind speed (see diagnostic number 28).

Z0 Surface Roughness Length ($ m$ )

Over the land surface, the surface roughness length is interpolated to the local time from the monthly mean data of Dorman and Sellers [1989]. Over the ocean, the roughness length is a function of the surface-stress velocity, $ u_*$ .

$\displaystyle {\bf Z0} = c_1u^3_* + c_2u^2_* + c_3u_* + c_4 + {c_5}{u_*} $

where the constants are chosen to interpolate between the reciprocal relation of Kondo [1975] for weak winds, and the piecewise linear relation of Large and Pond [1981] for moderate to large winds.

FRQTRB Frequency of Turbulence ($ 0-1$ )

The fraction of time when turbulence is present is defined as the fraction of time when the turbulent kinetic energy exceeds some minimum value, defined here to be $ 0.005 \hspace{.1cm}m^2/sec^2$ . When this criterion is met, a counter is incremented. The fraction over the averaging interval is reported.

PBL Planetary Boundary Layer Depth ($ mb$ )

The depth of the PBL is defined by the turbulence parameterization to be the depth at which the turbulent kinetic energy reduces to ten percent of its surface value.

$\displaystyle {\bf PBL} = P_{PBL} - P_{surface} $

where $ P_{PBL}$ is the pressure in $ mb$ at which the turbulent kinetic energy reaches one tenth of its surface value, and $ P_s$ is the surface pressure.

SWCLR Clear sky Heating Rate due to Shortwave Radiation ($ deg/day$ )

The net Shortwave heating rate is calculated as the vertical divergence of the net solar radiative fluxes. The clear-sky and cloudy-sky shortwave fluxes are calculated separately. For the clear-sky case, the shortwave fluxes and heating rates are computed with both CLMO (maximum overlap cloud fraction) and CLRO (random overlap cloud fraction) set to zero (see Section 6.5.3.2). The shortwave routine is then called a second time, for the cloudy-sky case, with the true time-averaged cloud fractions CLMO and CLRO being used. In all cases, a normalized incident shortwave flux is used as input at the top of the atmosphere.

The heating rate due to Shortwave Radiation under clear skies is defined as:

$\displaystyle \frac{\partial \rho c_p T}{\partial t} = - \frac{\partial }{\partial z} F(clear)_{SW}^{NET} \cdot {\rm RADSWT}, $

or

$\displaystyle {\bf SWCLR} = \frac{g}{c_p } \frac{\partial }{\partial p} F(clear)_{SW}^{NET}\cdot {\rm RADSWT} . $

where $ g$ is the accelation due to gravity, $ c_p$ is the heat capacity of air at constant pressure, RADSWT is the true incident shortwave radiation at the top of the atmosphere (See Diagnostic #48), and

$\displaystyle F(clear)_{SW}^{Net} = F(clear)_{SW}^\uparrow - F(clear)_{SW}^\downarrow $


OSR Net upward Shortwave flux at the top of the model ($ Watts/m^2$ )

$\displaystyle {\bf OSR} = F_{SW,top}^{NET} $

where top indicates the top of the first model layer used in the shortwave radiation routine. In the GCM, $ p_{SW_{top}}$ = 0 mb.

OSRCLR Net upward clearsky Shortwave flux at the top of the model ($ Watts/m^2$ )

$\displaystyle {\bf OSRCLR} = F(clearsky)_{SW,top}^{NET} $

where top indicates the top of the first model layer used in the shortwave radiation routine. In the GCM, $ p_{SW_{top}}$ = 0 mb.

CLDMAS Convective Cloud Mass Flux ($ kg / m^2$ )

The amount of cloud mass moved per RAS timestep from all convective clouds is written:

$\displaystyle {\bf CLDMAS} = \eta m_B $

where $ \eta $ is the entrainment, normalized by the cloud base mass flux, and $ m_B$ is the cloud base mass flux. $ m_B$ and $ \eta $ are defined explicitly in Section 6.5.3.2, the description of the convective parameterization.

UAVE Time-Averaged Zonal U-Wind ($ m/sec$ )

The diagnostic UAVE is simply the time-averaged Zonal U-Wind over the NUAVE output frequency. This is contrasted to the instantaneous Zonal U-Wind which is archived on the Prognostic Output data stream.

$\displaystyle {\bf UAVE} = u(\lambda, \phi, level , t) $


Note, UAVE is computed and stored on the staggered C-grid.

VAVE Time-Averaged Meridional V-Wind ($ m/sec$ )

The diagnostic VAVE is simply the time-averaged Meridional V-Wind over the NVAVE output frequency. This is contrasted to the instantaneous Meridional V-Wind which is archived on the Prognostic Output data stream.

$\displaystyle {\bf VAVE} = v(\lambda, \phi, level , t) $


Note, VAVE is computed and stored on the staggered C-grid.

TAVE Time-Averaged Temperature ($ Kelvin$ )

The diagnostic TAVE is simply the time-averaged Temperature over the NTAVE output frequency. This is contrasted to the instantaneous Temperature which is archived on the Prognostic Output data stream.

$\displaystyle {\bf TAVE} = T(\lambda, \phi, level , t) $


QAVE Time-Averaged Specific Humidity ($ g/kg$ )

The diagnostic QAVE is simply the time-averaged Specific Humidity over the NQAVE output frequency. This is contrasted to the instantaneous Specific Humidity which is archived on the Prognostic Output data stream.

$\displaystyle {\bf QAVE} = q(\lambda, \phi, level , t) $


PAVE Time-Averaged Surface Pressure - PTOP ($ mb$ )

The diagnostic PAVE is simply the time-averaged Surface Pressure - PTOP over the NPAVE output frequency. This is contrasted to the instantaneous Surface Pressure - PTOP which is archived on the Prognostic Output data stream.

$\displaystyle {\bf PAVE}$ $\displaystyle =$ $\displaystyle \pi(\lambda, \phi, level , t)$  
  $\displaystyle =$ $\displaystyle p_s(\lambda, \phi, level , t) - p_T$  


QQAVE Time-Averaged Turbulent Kinetic Energy $ (m/sec)^2$

The diagnostic QQAVE is simply the time-averaged prognostic Turbulent Kinetic Energy produced by the GCM Turbulence parameterization over the NQQAVE output frequency. This is contrasted to the instantaneous Turbulent Kinetic Energy which is archived on the Prognostic Output data stream.

$\displaystyle {\bf QQAVE} = qq(\lambda, \phi, level , t) $


Note, QQAVE is computed and stored at the ``mass-point'' locations on the staggered C-grid.

SWGCLR Net downward clearsky Shortwave flux at the surface ($ Watts/m^2$ )


$\displaystyle {\bf SWGCLR}$ $\displaystyle =$ $\displaystyle F(clearsky)_{SW,Nrphys+1}^{Net}$  
  $\displaystyle =$ $\displaystyle F(clearsky)_{SW,Nrphys+1}^\downarrow - F(clearsky)_{SW,Nrphys+1}^\uparrow$  


where Nrphys+1 indicates the lowest model edge-level, or $ p = p_{surf}$ . $ F(clearsky){SW}^\downarrow$ is the downward clearsky Shortwave flux and $ F(clearsky)_{SW}^\uparrow$ is the upward clearsky Shortwave flux.

DIABU Total Diabatic Zonal U-Wind Tendency ($ m/sec/day$ )

DIABU is the total time-tendency of the Zonal U-Wind due to Diabatic processes and the Analysis forcing.

$\displaystyle {\bf DIABU} = \frac{\partial u}{\partial t}_{Moist} + \frac{\partial u}{\partial t}_{Turbulence} + \frac{\partial u}{\partial t}_{Analysis} $


DIABV Total Diabatic Meridional V-Wind Tendency ($ m/sec/day$ )

DIABV is the total time-tendency of the Meridional V-Wind due to Diabatic processes and the Analysis forcing.

$\displaystyle {\bf DIABV} = \frac{\partial v}{\partial t}_{Moist} + \frac{\partial v}{\partial t}_{Turbulence} + \frac{\partial v}{\partial t}_{Analysis} $


DIABT Total Diabatic Temperature Tendency ($ deg/day$ )

DIABT is the total time-tendency of Temperature due to Diabatic processes and the Analysis forcing.

$\displaystyle {\bf DIABT}$ $\displaystyle =$ $\displaystyle \frac{\partial T}{\partial t}_{Moist Processes} + \frac{\partial T}{\partial t}_{Shortwave Radiation}$  
  $\displaystyle +$ $\displaystyle \frac{\partial T}{\partial t}_{Longwave Radiation} + \frac{\partial T}{\partial t}_{Turbulence} + \frac{\partial T}{\partial t}_{Analysis}$  


If we define the time-tendency of Temperature due to Diabatic processes as
$\displaystyle \frac{\partial T}{\partial t}_{Diabatic}$ $\displaystyle =$ $\displaystyle \frac{\partial T}{\partial t}_{Moist Processes} + \frac{\partial T}{\partial t}_{Shortwave Radiation}$  
  $\displaystyle +$ $\displaystyle \frac{\partial T}{\partial t}_{Longwave Radiation} + \frac{\partial T}{\partial t}_{Turbulence}$  

then, since there are no surface pressure changes due to Diabatic processes, we may write

$\displaystyle \frac{\partial T}{\partial t}_{Diabatic} = \frac{p^\kappa}{\pi}\frac{\partial \pi \theta}{\partial t}_{Diabatic} $

where $ \theta = T/p^\kappa$ . Thus, DIABT may be written as

$\displaystyle {\bf DIABT} = \frac{p^\kappa}{\pi} \left( \frac{\partial \pi \the... ...tial t}_{Diabatic} + \frac{\partial \pi \theta}{\partial t}_{Analysis} \right) $


DIABQ Total Diabatic Specific Humidity Tendency ($ g/kg/day$ )

DIABQ is the total time-tendency of Specific Humidity due to Diabatic processes and the Analysis forcing.

$\displaystyle {\bf DIABQ} = \frac{\partial q}{\partial t}_{Moist Processes} + \... ...artial q}{\partial t}_{Turbulence} + \frac{\partial q}{\partial t}_{Analysis} $

If we define the time-tendency of Specific Humidity due to Diabatic processes as

$\displaystyle \frac{\partial q}{\partial t}_{Diabatic} = \frac{\partial q}{\partial t}_{Moist Processes} + \frac{\partial q}{\partial t}_{Turbulence} $

then, since there are no surface pressure changes due to Diabatic processes, we may write

$\displaystyle \frac{\partial q}{\partial t}_{Diabatic} = \frac{1}{\pi}\frac{\partial \pi q}{\partial t}_{Diabatic} $

Thus, DIABQ may be written as

$\displaystyle {\bf DIABQ} = \frac{1}{\pi} \left( \frac{\partial \pi q}{\partial t}_{Diabatic} + \frac{\partial \pi q}{\partial t}_{Analysis} \right) $


VINTUQ Vertically Integrated Moisture Flux ( $ m/sec \cdot g/kg$ )

The vertically integrated moisture flux due to the zonal u-wind is obtained by integrating $ u q$ over the depth of the atmosphere at each model timestep, and dividing by the total mass of the column.

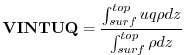
$\displaystyle {\bf VINTUQ} = \frac{ \int_{surf}^{top} u q \rho dz } { \int_{surf}^{top} \rho dz } $

Using $ \rho \delta z = -\frac{\delta p}{g} = - \frac{1}{g} \delta p$ , we have

$\displaystyle {\bf VINTUQ} = { \int_0^1 u q dp } $


VINTVQ Vertically Integrated Moisture Flux ( $ m/sec \cdot g/kg$ )

The vertically integrated moisture flux due to the meridional v-wind is obtained by integrating $ v q$ over the depth of the atmosphere at each model timestep, and dividing by the total mass of the column.

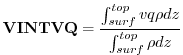
$\displaystyle {\bf VINTVQ} = \frac{ \int_{surf}^{top} v q \rho dz } { \int_{surf}^{top} \rho dz } $

Using $ \rho \delta z = -\frac{\delta p}{g} = - \frac{1}{g} \delta p$ , we have

$\displaystyle {\bf VINTVQ} = { \int_0^1 v q dp } $


VINTUT Vertically Integrated Heat Flux ( $ m/sec \cdot deg$ )

The vertically integrated heat flux due to the zonal u-wind is obtained by integrating $ u T$ over the depth of the atmosphere at each model timestep, and dividing by the total mass of the column.

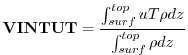
$\displaystyle {\bf VINTUT} = \frac{ \int_{surf}^{top} u T \rho dz } { \int_{surf}^{top} \rho dz } $

Or,

$\displaystyle {\bf VINTUT} = { \int_0^1 u T dp } $


VINTVT Vertically Integrated Heat Flux ( $ m/sec \cdot deg$ )

The vertically integrated heat flux due to the meridional v-wind is obtained by integrating $ v T$ over the depth of the atmosphere at each model timestep, and dividing by the total mass of the column.

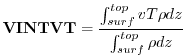
$\displaystyle {\bf VINTVT} = \frac{ \int_{surf}^{top} v T \rho dz } { \int_{surf}^{top} \rho dz } $

Using $ \rho \delta z = -\frac{\delta p}{g} $ , we have

$\displaystyle {\bf VINTVT} = { \int_0^1 v T dp } $


CLDFRC Total 2-Dimensional Cloud Fracton ($ 0-1$ )

If we define the time-averaged random and maximum overlapped cloudiness as CLRO and CLMO respectively, then the probability of clear sky associated with random overlapped clouds at any level is (1-CLRO) while the probability of clear sky associated with maximum overlapped clouds at any level is (1-CLMO). The total clear sky probability is given by (1-CLRO)*(1-CLMO), thus the total cloud fraction at each level may be obtained by 1-(1-CLRO)*(1-CLMO).

At any given level, we may define the clear line-of-site probability by appropriately accounting for the maximum and random overlap cloudiness. The clear line-of-site probability is defined to be equal to the product of the clear line-of-site probabilities associated with random and maximum overlap cloudiness. The clear line-of-site probability $ C(p,p^{\prime})$ associated with maximum overlap clouds, from the current pressure $ p$ to the model top pressure, $ p^{\prime} = p_{top}$ , or the model surface pressure, $ p^{\prime} = p_{surf}$ , is simply 1.0 minus the largest maximum overlap cloud value along the line-of-site, ie.

$\displaystyle 1-MAX_p^{p^{\prime}} \left( CLMO_p \right)$

Thus, even in the time-averaged sense it is assumed that the maximum overlap clouds are correlated in the vertical. The clear line-of-site probability associated with random overlap clouds is defined to be the product of the clear sky probabilities at each level along the line-of-site, ie.

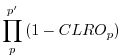
$\displaystyle \prod_{p}^{p^{\prime}} \left( 1-CLRO_p \right)$

The total cloud fraction at a given level associated with a line- of-site calculation is given by

$\displaystyle 1-\left( 1-MAX_p^{p^{\prime}} \left[ CLMO_p \right] \right) \prod_p^{p^{\prime}} \left( 1-CLRO_p \right)$

The 2-dimensional net cloud fraction as seen from the top of the atmosphere is given by

$\displaystyle {\bf CLDFRC} = 1-\left( 1-MAX_{l=l_1}^{Nrphys} \left[ CLMO_l \right] \right) \prod_{l=l_1}^{Nrphys} \left( 1-CLRO_l \right) $


For a complete description of cloud/radiative interactions, see Section 6.5.3.2.

QINT Total Precipitable Water ($ gm/cm^2$ )

The Total Precipitable Water is defined as the vertical integral of the specific humidity, given by:

$\displaystyle {\bf QINT}$ $\displaystyle =$ $\displaystyle \int_{surf}^{top} \rho q dz$  
  $\displaystyle =$ $\displaystyle \frac{\pi}{g} \int_0^1 q dp$  

where we have used the hydrostatic relation $ \rho \delta z = -\frac{\delta p}{g} $ .

U2M Zonal U-Wind at 2 Meter Depth ($ m/sec$ )

The u-wind at the 2-meter depth is determined from the similarity theory:

$\displaystyle {\bf U2M} = \frac{u_*}{k} \psi_{m_{2m}} \frac{u_{sl}}{W_s} = \frac{ \psi_{m_{2m}} }{ \psi_{m_{sl}} }u_{sl} $

where $ \psi_m(2m)$ is the non-dimensional wind shear at two meters, and the subscript $ sl$ refers to the height of the top of the surface layer. If the roughness height is above two meters, $ {\bf U2M}$ is undefined.

V2M Meridional V-Wind at 2 Meter Depth ($ m/sec$ )

The v-wind at the 2-meter depth is a determined from the similarity theory:

$\displaystyle {\bf V2M} = \frac{u_*}{k} \psi_{m_{2m}} \frac{v_{sl}}{W_s} = \frac{ \psi_{m_{2m}} }{ \psi_{m_{sl}} }v_{sl} $

where $ \psi_m(2m)$ is the non-dimensional wind shear at two meters, and the subscript $ sl$ refers to the height of the top of the surface layer. If the roughness height is above two meters, $ {\bf V2M}$ is undefined.

T2M Temperature at 2 Meter Depth ( $ deg \hspace{.1cm} K$ )

The temperature at the 2-meter depth is a determined from the similarity theory:

$\displaystyle {\bf T2M} = P^{\kappa} (\frac{\theta*}{k} ({\psi_{h_{2m}}+\psi_g}... ...psi_{h_{2m}}+\psi_g }{ \psi_{h_{sl}}+\psi_g } (\theta_{sl} - \theta_{surf}) ) $

where:

$\displaystyle \theta_* = - \frac{ (\overline{w^{\prime}\theta^{\prime}}) }{ u_* } $

where $ \psi_h(2m)$ is the non-dimensional temperature gradient at two meters, $ \psi_g$ is the non-dimensional temperature gradient in the viscous sublayer, and the subscript $ sl$ refers to the height of the top of the surface layer. If the roughness height is above two meters, $ {\bf T2M}$ is undefined.

Q2M Specific Humidity at 2 Meter Depth ($ g/kg$ )

The specific humidity at the 2-meter depth is determined from the similarity theory:

$\displaystyle {\bf Q2M} = P^{\kappa} \frac({q_*}{k} ({\psi_{h_{2m}}+\psi_g}) + ... ... + \frac{ \psi_{h_{2m}}+\psi_g }{ \psi_{h_{sl}}+\psi_g } (q_{sl} - q_{surf})) $

where:

$\displaystyle q_* = - \frac{ (\overline{w^{\prime}q^{\prime}}) }{ u_* } $

where $ \psi_h(2m)$ is the non-dimensional temperature gradient at two meters, $ \psi_g$ is the non-dimensional temperature gradient in the viscous sublayer, and the subscript $ sl$ refers to the height of the top of the surface layer. If the roughness height is above two meters, $ {\bf Q2M}$ is undefined.

U10M Zonal U-Wind at 10 Meter Depth ($ m/sec$ )

The u-wind at the 10-meter depth is an interpolation between the surface wind and the model lowest level wind using the ratio of the non-dimensional wind shear at the two levels:

$\displaystyle {\bf U10M} = \frac{u_*}{k} \psi_{m_{10m}} \frac{u_{sl}}{W_s} = \frac{ \psi_{m_{10m}} }{ \psi_{m_{sl}} }u_{sl} $

where $ \psi_m(10m)$ is the non-dimensional wind shear at ten meters, and the subscript $ sl$ refers to the height of the top of the surface layer.

V10M Meridional V-Wind at 10 Meter Depth ($ m/sec$ )

The v-wind at the 10-meter depth is an interpolation between the surface wind and the model lowest level wind using the ratio of the non-dimensional wind shear at the two levels:

$\displaystyle {\bf V10M} = \frac{u_*}{k} \psi_{m_{10m}} \frac{v_{sl}}{W_s} = \frac{ \psi_{m_{10m}} }{ \psi_{m_{sl}} }v_{sl} $

where $ \psi_m(10m)$ is the non-dimensional wind shear at ten meters, and the subscript $ sl$ refers to the height of the top of the surface layer.

T10M Temperature at 10 Meter Depth ( $ deg \hspace{.1cm} K$ )

The temperature at the 10-meter depth is an interpolation between the surface potential temperature and the model lowest level potential temperature using the ratio of the non-dimensional temperature gradient at the two levels:

$\displaystyle {\bf T10M} = P^{\kappa} (\frac{\theta*}{k} ({\psi_{h_{10m}}+\psi_... ...c{\psi_{h_{10m}}+\psi_g}{\psi_{h_{sl}}+\psi_g} (\theta_{sl} - \theta_{surf})) $

where:

$\displaystyle \theta_* = - \frac{ (\overline{w^{\prime}\theta^{\prime}}) }{ u_* } $

where $ \psi_h(10m)$ is the non-dimensional temperature gradient at two meters, $ \psi_g$ is the non-dimensional temperature gradient in the viscous sublayer, and the subscript $ sl$ refers to the height of the top of the surface layer.

Q10M Specific Humidity at 10 Meter Depth ($ g/kg$ )

The specific humidity at the 10-meter depth is an interpolation between the surface specific humidity and the model lowest level specific humidity using the ratio of the non-dimensional temperature gradient at the two levels:

$\displaystyle {\bf Q10M} = P^{\kappa} (\frac{q_*}{k} ({\psi_{h_{10m}}+\psi_g}) ... ...rf} + \frac{\psi_{h_{10m}}+\psi_g}{\psi_{h_{sl}}+\psi_g} (q_{sl} - q_{surf})) $

where:

$\displaystyle q_* = - \frac{ (\overline{w^{\prime}q^{\prime}}) }{ u_* } $

where $ \psi_h(10m)$ is the non-dimensional temperature gradient at two meters, $ \psi_g$ is the non-dimensional temperature gradient in the viscous sublayer, and the subscript $ sl$ refers to the height of the top of the surface layer.

DTRAIN Cloud Detrainment Mass Flux ($ kg / m^2$ )

The amount of cloud mass moved per RAS timestep at the cloud detrainment level is written:

$\displaystyle {\bf DTRAIN} = \eta_{r_D}m_B $

where $ r_D$ is the detrainment level, $ m_B$ is the cloud base mass flux, and $ \eta $ is the entrainment, defined in Section 6.5.3.2.

QFILL Filling of negative Specific Humidity ($ g/kg/day$ )

Due to computational errors associated with the numerical scheme used for the advection of moisture, negative values of specific humidity may be generated. The specific humidity is checked for negative values after every dynamics timestep. If negative values have been produced, a filling algorithm is invoked which redistributes moisture from below. Diagnostic QFILL is equal to the net filling needed to eliminate negative specific humidity, scaled to a per-day rate:

$\displaystyle {\bf QFILL} = q^{n+1}_{final} - q^{n+1}_{initial} $

where

$\displaystyle q^{n+1} = (\pi q)^{n+1} / \pi^{n+1} $

6.5.3.4 Key subroutines, parameters and files

6.5.3.5 Dos and donts

6.5.3.6 Fizhi Reference


6.5.3.7 Experiments and tutorials that use fizhi

  • Global atmosphere experiment with realistic SST and topography in fizhi-cs-32x32x10 verification directory.
  • Global atmosphere aqua planet experiment in fizhi-cs-aqualev20 verification directory.

next up previous contents
Next: 6.6 Sea Ice Packages Up: 6.5 Atmosphere Packages Previous: 6.5.2 Land package   Contents
mitgcm-support@mitgcm.org
Copyright © 2006 Massachusetts Institute of Technology Last update 2011-01-09