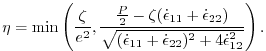6.6.2 SEAICE Package

About

Installation

Tutorials

Documentation

1.1 Introduction

1.3 Continuous equations in `r' coordinates

2. Discretization and Algorithm

4. Software Architecture

5. Automatic Differentiation

6. Physical Parameterization and Packages

7. Diagnostics and tools

8. Interface with ECCO

Browse Code

PDF file (9Mb)

PS file (7Mb)

Next: 6.6.3 SHELFICE Package Up: 6.6 Sea Ice Packages Previous: 6.6.1 THSICE: The Thermodynamic Contents

Subsections

6.6.2 SEAICE Package

Authors: Martin Losch, Dimitris Menemenlis, An Nguyen, Jean-Michel Campin, Patrick Heimbach, Chris Hill and Jinlun Zhang

6.6.2.1 Introduction

Package ``seaice'' provides a dynamic and thermodynamic interactive sea-ice model.

CPP options enable or disable different aspects of the package (Section 6.6.2.2). Run-Time options, flags, filenames and field-related dates/times are set in data.seaice (Section 6.6.2.3). A description of key subroutines is given in Section 6.6.2.5. Input fields, units and sign conventions are summarized in Section 6.6.2.3, and available diagnostics output is listed in Section 6.6.2.6.

6.6.2.2 SEAICE configuration, compiling & running

6.6.2.2.1 Compile-time options

As with all MITgcm packages, SEAICE can be turned on or off at compile time

using the packages.conf file by adding seaice to it,
or using genmake2 adding -enable=seaice or -disable=seaice switches
required packages and CPP options:
SEAICE requires the external forcing package exf to be enabled; no additional CPP options are required.

(see Section 3.4).

Parts of the SEAICE code can be enabled or disabled at compile time via CPP preprocessor flags. These options are set in either SEAICE_OPTIONS.h or in ECCO_CPPOPTIONS.h. Table 6.6.2.2 summarizes these options.

CPP option	Description
`SEAICE_DEBUG`	Enhance STDOUT for debugging
`SEAICE_ALLOW_DYNAMICS`	sea-ice dynamics code
`SEAICE_CGRID`	LSR solver on C-grid (rather than original B-grid)
`SEAICE_ALLOW_EVP`	use EVP rather than LSR rheology solver
`SEAICE_EXTERNAL_FLUXES`	use EXF-computed fluxes as starting point
`SEAICE_MULTICATEGORY`	enable 8-category thermodynamics (by default undefined)
`SEAICE_VARIABLE_FREEZING_POINT`	enable linear dependence of the freezing point on salinity (by default undefined)
`ALLOW_SEAICE_FLOODING`	enable snow to ice conversion for submerged sea-ice
`SEAICE_SALINITY`	enable "salty" sea-ice (by default undefined)
`SEAICE_AGE`	enable "age tracer" sea-ice (by default undefined)
`SEAICE_CAP_HEFF`	enable capping of sea-ice thickness to MAX_HEFF
`SEAICE_BICE_STRESS`	B-grid only for backward compatiblity: turn on ice-stress on ocean
`EXPLICIT_SSH_SLOPE`	B-grid only for backward compatiblity: use ETAN for tilt computations rather than geostrophic velocities

6.6.2.3 Run-time parameters

Run-time parameters are set in files data.pkg (read in packages_readparms.F), and data.seaice (read in seaice_readparms.F).

6.6.2.3.1 Enabling the package

A package is switched on/off at run-time by setting (e.g. for SEAICE) useSEAICE = .TRUE. in data.pkg.

6.6.2.3.2 General flags and parameters

Table 6.17 lists most run-time parameters.

**Table 6.17:** Run-time parameters and default values

Name	Default value	Description	Reference

SEAICEwriteState	T	write sea ice state to file
SEAICEuseDYNAMICS	T	use dynamics
SEAICEuseTEM	F	use truncated ellipse method
SEAICEuseMetricTerms	T	use metric terms in dynamics
SEAICEuseEVPpickup	T	use EVP pickups
SEAICEuseFluxForm	F	use flux form for 2nd central difference advection scheme
SEAICErestoreUnderIce	F	enable restoring to climatology under ice
useHB87stressCoupling	F	turn on ice-ocean stress coupling following Hibler and Bryan [1987]
usePW79thermodynamics	T	flag to turn off zero-layer-thermodynamics for testing
SEAICEadvHeff/Area/Snow/Salt/Age	T	flag to turn off advection of scalar state variables
SEAICEuseFlooding	T	use flood-freeze algorithm
SEAICE_no_slip	F	switch between free-slip and no-slip boundary conditions
LAD	2	time stepping scheme
IMAX_TICE	10	iterations for ice heat budget
SEAICE_deltaTtherm	dTracerLev(1)	thermodynamic timestep
SEAICE_deltaTdyn	dTracerLev(1)	dynamic timestep
SEAICE_dumpFreq	dumpFreq	dump frequency
SEAICE_taveFreq	taveFreq	time-averaging frequency
SEAICE_dump_mdsio	T	write snap-shot using MDSIO
SEAICE_tave_mdsio	T	write TimeAverage using MDSIO
SEAICE_dump_mnc	F	write snap-shot using MNC
SEAICE_tave_mnc	F	write TimeAverage using MNC
SEAICE_initialHEFF	0.00000E+00	initial sea-ice thickness
SEAICE_drag	2.00000E-03	air-ice drag coefficient
OCEAN_drag	1.00000E-03	air-ocean drag coefficient
SEAICE_waterDrag	5.50000E+00	water-ice drag
SEAICE_dryIceAlb	7.50000E-01	winter albedo
SEAICE_wetIceAlb	6.60000E-01	summer albedo
SEAICE_drySnowAlb	8.40000E-01	dry snow albedo
SEAICE_wetSnowAlb	7.00000E-01	wet snow albedo
SEAICE_waterAlbedo	1.00000E-01	water albedo
SEAICE_strength	2.75000E+04	sea-ice strength Pstar
SEAICE_sensHeat	2.28400E+00	sensible heat transfer (1.75E-03 * 1004 * 1.3)
SEAICE_latentWater	5.68750E+03	latent heat transfer for water (1.75E-03 * 2.5E+06 * 1.3)
SEAICE_latentIce	6.44740E+03	latent heat transfer for ice (1.75E-03 * 2.834E+06 * 1.3)
SEAICE_iceConduct	2.16560E+00	sea-ice conductivity
SEAICE_snowConduct	3.10000E-01	snow conductivity
SEAICE_emissivity	5.50000E-08	Stefan-Boltzman
SEAICE_snowThick	1.50000E-01	cutoff snow thickness
SEAICE_shortwave	3.00000E-01	penetration shortwave radiation
SEAICE_freeze	-1.96000E+00	freezing temp. of sea water
SEAICE_salinity	0.0	salinity of ice
SEAICE_gamma_t	UNSET	restoring time scale for basal freezing and melting
SEAICE_gamma_t_frz	UNSET	restoring time scale for basal freezing
SEAICEstressFactor	1.00000E+00	scaling factor for ice-ocean stress
Heff/Area/Hsnow/Hsalt/IceAgeFile	UNSET	initial fields for variables HEFF/AREA/HSNOW/HSALT/ICEAGE
LSR_ERROR	1.00000E-04	sets accuracy of LSR solver
DIFF1	4.00000E-03	parameter used in advect.F
A22	1.50000E-01	parameter used in growth.F
HO	5.00000E-01	demarcation ice thickness
MAX_HEFF	1.00000E+01	maximum ice thickness
MIN_ATEMP	-5.00000E+01	minimum air temperature
MIN_LWDOWN	6.00000E+01	minimum downward longwave
MAX_TICE	3.00000E+01	maximum ice temperature
MIN_TICE	-5.00000E+01	minimum ice temperature
SEAICE_EPS	1.00000E-10	reduce derivative singularities

6.6.2.3.3 Input fields and units

HeffFile:: Initial sea ice thickness averaged over grid cell in meters; initializes variable HEFF;
AreaFile:: Initial fractional sea ice cover, range ; initializes variable AREA;
HsnowFile:: Initial snow thickness on sea ice averaged over grid cell in meters; initializes variable HSNOW;
HsaltFile:: Initial salinity of sea ice averaged over grid cell in g/m ; initializes variable HSALT;
IceAgeFile:: Initial ice age of sea ice averaged over grid cell in seconds; initializes variable ICEAGE;

6.6.2.4 Description

[TO BE CONTINUED/MODIFIED]

The MITgcm sea ice model (MITgcm/sim) is based on a variant of the viscous-plastic (VP) dynamic-thermodynamic sea ice model [Zhang and Hibler, 1997] first introduced by Hibler [1980,1979]. In order to adapt this model to the requirements of coupled ice-ocean state estimation, many important aspects of the original code have been modified and improved:

the code has been rewritten for an Arakawa C-grid, both B- and C-grid variants are available; the C-grid code allows for no-slip and free-slip lateral boundary conditions;
two different solution methods for solving the nonlinear momentum equations have been adopted: LSOR [Zhang and Hibler, 1997], and EVP [Hunke and Dukowicz, 1997];
ice-ocean stress can be formulated as in Hibler and Bryan [1987] or as in Campin et al. [2008];
ice variables are advected by sophisticated, conservative advection schemes with flux limiting;
growth and melt parameterizations have been refined and extended in order to allow for more stable automatic differentiation of the code.

The sea ice model is tightly coupled to the ocean compontent of the MITgcm. Heat, fresh water fluxes and surface stresses are computed from the atmospheric state and - by default - modified by the ice model at every time step.

The ice dynamics models that are most widely used for large-scale climate studies are the viscous-plastic (VP) model [Hibler, 1979], the cavitating fluid (CF) model [Flato and Hibler, 1992], and the elastic-viscous-plastic (EVP) model [Hunke and Dukowicz, 1997]. Compared to the VP model, the CF model does not allow ice shear in calculating ice motion, stress, and deformation. EVP models approximate VP by adding an elastic term to the equations for easier adaptation to parallel computers. Because of its higher accuracy in plastic solution and relatively simpler formulation, compared to the EVP model, we decided to use the VP model as the default dynamic component of our ice model. To do this we extended the line successive over relaxation (LSOR) method of Zhang and Hibler [1997] for use in a parallel configuration.

Note, that by default the seaice-package includes the orginial so-called zero-layer thermodynamics following Hibler [1980] with a snow cover as in Zhang et al. [1998]. The zero-layer thermodynamic model assumes that ice does not store heat and, therefore, tends to exaggerate the seasonal variability in ice thickness. This exaggeration can be significantly reduced by using Semtner's [1976] three-layer thermodynamic model that permits heat storage in ice. Recently, the three-layer thermodynamic model has been reformulated by Winton [2000]. The reformulation improves model physics by representing the brine content of the upper ice with a variable heat capacity. It also improves model numerics and consumes less computer time and memory. The Winton sea-ice thermodynamics have been ported to the MIT GCM; they currently reside under pkg/thsice. The package pkg/thsice is fully compatible with pkg/seaice and with pkg/exf. When turned on together with pkg/seaice, the zero-layer thermodynamics are replaced by the Winton thermodynamics.

The sea ice model requires the following input fields: 10-m winds, 2-m air temperature and specific humidity, downward longwave and shortwave radiations, precipitation, evaporation, and river and glacier runoff. The sea ice model also requires surface temperature from the ocean model and the top level horizontal velocity. Output fields are surface wind stress, evaporation minus precipitation minus runoff, net surface heat flux, and net shortwave flux. The sea-ice model is global: in ice-free regions bulk formulae are used to estimate oceanic forcing from the atmospheric fields.

6.6.2.4.1 Dynamics

The momentum equation of the sea-ice model is

$\displaystyle m \frac{D\ensuremath{\vec{\mathbf{u}}}}{Dt} = -mf\ensuremath{\vec... ...f{\mathbf{\tau}}}}_{ocean} - m \nabla{\phi(0)} + \ensuremath{\vec{\mathbf{F}}},$

(6.34)

where $m=m_{i}+m_{s}$ is the ice and snow mass per unit area; $\ensuremath{\vec{\mathbf{u}}}=u\ensuremath{\vec{\mathbf{i}}}+v\ensuremath{\vec{\mathbf{j}}}$ is the ice velocity vector; $\ensuremath{\vec{\mathbf{i}}}$ , $\ensuremath{\vec{\mathbf{j}}}$ , and $\ensuremath{\vec{\mathbf{k}}}$ are unit vectors in the

, and

directions, respectively;

is the Coriolis parameter; $\ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{air}$ and $\ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{ocean}$ are the wind-ice and ocean-ice stresses, respectively;

is the gravity accelation; $\nabla\phi(0)$ is the gradient (or tilt) of the sea surface height; $\phi(0) = g\eta + p_{a}/\rho_{0} + mg/\rho_{0}$ is the sea surface height potential in response to ocean dynamics ( $g\eta$ ), to atmospheric pressure loading ( $p_{a}/\rho_{0}$ , where $\rho_{0}$ is a reference density) and a term due to snow and ice loading [Campin et al., 2008]; and $\ensuremath{\vec{\mathbf{F}}}=\nabla\cdot\sigma$ is the divergence of the internal ice stress tensor $\sigma_{ij}$ . Advection of sea-ice momentum is neglected. The wind and ice-ocean stress terms are given by

$\displaystyle \ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{air} =$	$\displaystyle \rho_{air} C_{air} \vert\ensuremath{\vec{\mathbf{U}}}_{air} -\ens... ...t R_{air} (\ensuremath{\vec{\mathbf{U}}}_{air} -\ensuremath{\vec{\mathbf{u}}}),$
$\displaystyle \ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{ocean} =$	$\displaystyle \rho_{ocean}C_{ocean} \vert\ensuremath{\vec{\mathbf{U}}}_{ocean}-... ...R_{ocean}(\ensuremath{\vec{\mathbf{U}}}_{ocean}-\ensuremath{\vec{\mathbf{u}}}),$

where $\ensuremath{\vec{\mathbf{U}}}_{air/ocean}$ are the surface winds of the atmosphere and surface currents of the ocean, respectively; $C_{air/ocean}$ are air and ocean drag coefficients; $\rho_{air/ocean}$ are reference densities; and $R_{air/ocean}$ are rotation matrices that act on the wind/current vectors.

For an isotropic system the stress tensor $\sigma_{ij}$ ( ) can be related to the ice strain rate and strength by a nonlinear viscous-plastic (VP) constitutive law [Hibler, 1979; Zhang and Hibler, 1997]:

$\displaystyle \sigma_{ij}=2\eta(\dot{\epsilon}_{ij},P)\dot{\epsilon}_{ij} + \le... ...epsilon}_{ij},P)\right]\dot{\epsilon}_{kk}\delta_{ij} - \frac{P}{2}\delta_{ij}.$

(6.35)

The ice strain rate is given by

$\displaystyle \dot{\epsilon}_{ij} = \frac{1}{2}\left( \frac{\partial{u_{i}}}{\partial{x_{j}}} + \frac{\partial{u_{j}}}{\partial{x_{i}}}\right).$

The maximum ice pressure $P_{\max}$ , a measure of ice strength, depends on both thickness

and compactness (concentration)

$\displaystyle P_{\max} = P^{*}c\,h\,e^{[C^{*}\cdot(1-c)]},$

(6.36)

with the constants $P^{*}$ (run-time parameter SEAICE_strength) and $C^{*}=20$ . The nonlinear bulk and shear viscosities $\eta$ and $\zeta$ are functions of ice strain rate invariants and ice strength such that the principal components of the stress lie on an elliptical yield curve with the ratio of major to minor axis

equal to

; they are given by:

$\displaystyle \zeta =$	$\displaystyle \min\left(\frac{P_{\max}}{2\max(\Delta,\Delta_{\min})}, \zeta_{\max}\right)$
$\displaystyle \eta =$	$\displaystyle \frac{\zeta}{e^2}$
with the abbreviation
$\displaystyle \Delta =$	$\displaystyle \left[ \left(\dot{\epsilon}_{11}^2+\dot{\epsilon}_{22}^2\right) (... ...}^2 + 2\dot{\epsilon}_{11}\dot{\epsilon}_{22} (1-e^{-2}) \right]^{\frac{1}{2}}.$

The bulk viscosities are bounded above by imposing both a minimum $\Delta_{\min}$ (for numerical reasons, run-time parameter SEAICE_EPS with a default value of $10^{-10}$ s $^{-1}$ ) and a maximum $\zeta_{\max} = P_{\max}/\Delta^*$ , where $\Delta^*=(5\times10^{12}/2\times10^4)$ s $^{-1}$ . (There is also the option of bounding $\zeta$ from below by setting run-time parameter SEAICE_zetaMin

, but this is generally not recommended). For stress tensor computation the replacement pressure $P = 2\,\Delta\zeta$ [Hibler and Ip, 1995] is used so that the stress state always lies on the elliptic yield curve by definition.

In the so-called truncated ellipse method the shear viscosity $\eta$ is capped to suppress any tensile stress [Geiger et al., 1998; Hibler and Schulson, 1997]:

$\displaystyle \eta = \min\left(\frac{\zeta}{e^2}, \frac{\frac{P}{2}-\zeta(\dot{... ...t{(\dot{\epsilon}_{11}+\dot{\epsilon}_{22})^2 +4\dot{\epsilon}_{12}^2}}\right).$

(6.37)

To enable this method, set #define SEAICE_ALLOW_TEM in SEAICE_OPTIONS.h and turn it on with SEAICEuseTEM=.TRUE. in data.seaice.

In the current implementation, the VP-model is integrated with the semi-implicit line successive over relaxation (LSOR)-solver of Zhang and Hibler [1997], which allows for long time steps that, in our case, are limited by the explicit treatment of the Coriolis term. The explicit treatment of the Coriolis term does not represent a severe limitation because it restricts the time step to approximately the same length as in the ocean model where the Coriolis term is also treated explicitly.

Hunke and Dukowicz [1997]'s introduced an elastic contribution to the strain rate in order to regularize Eq. 6.36 in such a way that the resulting elastic-viscous-plastic (EVP) and VP models are identical at steady state,

$\displaystyle \frac{1}{E}\frac{\partial\sigma_{ij}}{\partial{t}} + \frac{1}{2\e... ...eta}\sigma_{kk}\delta_{ij} + \frac{P}{4\zeta}\delta_{ij} = \dot{\epsilon}_{ij}.$

(6.38)

The EVP-model uses an explicit time stepping scheme with a short timestep. According to the recommendation of Hunke and Dukowicz [1997], the EVP-model is stepped forward in time 120 times within the physical ocean model time step (although this parameter is under debate), to allow for elastic waves to disappear. Because the scheme does not require a matrix inversion it is fast in spite of the small internal timestep and simple to implement on parallel computers [Hunke and Dukowicz, 1997]. For completeness, we repeat the equations for the components of the stress tensor $\sigma_{1} = \sigma_{11}+\sigma_{22}$ , $\sigma_{2}= \sigma_{11}-\sigma_{22}$ , and $\sigma_{12}$ . Introducing the divergence $D_D = \dot{\epsilon}_{11}+\dot{\epsilon}_{22}$ , and the horizontal tension and shearing strain rates, $D_T = \dot{\epsilon}_{11}-\dot{\epsilon}_{22}$ and $D_S = 2\dot{\epsilon}_{12}$ , respectively, and using the above abbreviations, the equations 6.39 can be written as:

$\displaystyle \frac{\partial\sigma_{1}}{\partial{t}} + \frac{\sigma_{1}}{2T} + \frac{P}{2T}$	$\displaystyle = \frac{P}{2T\Delta} D_D$	(6.39)
$\displaystyle \frac{\partial\sigma_{2}}{\partial{t}} + \frac{\sigma_{2} e^{2}}{2T}$	$\displaystyle = \frac{P}{2T\Delta} D_T$	(6.40)
$\displaystyle \frac{\partial\sigma_{12}}{\partial{t}} + \frac{\sigma_{12} e^{2}}{2T}$	$\displaystyle = \frac{P}{4T\Delta} D_S$	(6.41)

Here, the elastic parameter

is redefined in terms of a damping timescale

for elastic waves

$\displaystyle E=\frac{\zeta}{T}.$

$T=E_{0}\Delta{t}$ with the tunable parameter

and the external (long) timestep $\Delta{t}$ . Hunke and Dukowicz [1997] recommend $E_{0} = \frac{1}{3}$ (which is the default value in the code).

To use the EVP solver, make sure that both SEAICE_CGRID and SEAICE_ALLOW_EVP are defined in SEAICE_OPTIONS.h (default). The solver is turned on by setting the sub-cycling time step SEAICE_deltaTevp to a value larger than zero. The choice of this time step is under debate. Hunke and Dukowicz [1997] recommend order(120) time steps for the EVP solver within one model time step $\Delta{t}$ (deltaTmom). One can also choose order(120) time steps within the forcing time scale, but then we recommend adjusting the damping time scale accordingly, by setting either SEAICE_elasticParm ( $E_{0}$ ), so that $E_{0}\Delta{t}=$ forcing time scale , or directly SEAICE_evpTauRelax ( ) to the forcing time scale.

Moving sea ice exerts a stress on the ocean which is the opposite of the stress $\ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{ocean}$ in Eq. 6.35. This stess is applied directly to the surface layer of the ocean model. An alternative ocean stress formulation is given by Hibler and Bryan [1987]. Rather than applying $\ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{ocean}$ directly, the stress is derived from integrating over the ice thickness to the bottom of the oceanic surface layer. In the resulting equation for the combined ocean-ice momentum, the interfacial stress cancels and the total stress appears as the sum of windstress and divergence of internal ice stresses: $\delta(z) (\ensuremath{\vec{\mathbf{\mathbf{\tau}}}}_{air} + \ensuremath{\vec{\mathbf{F}}})/\rho_0$ , [see also Eq.2 of Hibler and Bryan, 1987]. The disadvantage of this formulation is that now the velocity in the surface layer of the ocean that is used to advect tracers, is really an average over the ocean surface velocity and the ice velocity leading to an inconsistency as the ice temperature and salinity are different from the oceanic variables. To turn on the stress formulation of Hibler and Bryan [1987], set useHB87StressCoupling=.TRUE. in data.seaice.

6.6.2.4.2 Finite-volume discretization of the stress tensor divergence

On an Arakawa C grid, ice thickness and concentration and thus ice strength

and bulk and shear viscosities $\zeta$ and $\eta$ are naturally defined a C-points in the center of the grid cell. Discretization requires only averaging of $\zeta$ and $\eta$ to vorticity or Z-points (or $\zeta$ -points, but here we use Z in order avoid confusion with the bulk viscosity) at the bottom left corner of the cell to give $\overline{\zeta}^{Z}$ and $\overline{\eta}^{Z}$ . In the following, the superscripts indicate location at Z or C points, distance across the cell (F), along the cell edge (G), between

-points (U),

-points (V), and C-points (C). The control volumes of the

- and

-equations in the grid cell at indices

are $A_{i,j}^{w}$ and $A_{i,j}^{s}$ , respectively. With these definitions (which follow the model code documentation except that $\zeta$ -points have been renamed to Z-points), the strain rates are discretized as:

$\displaystyle \dot{\epsilon}_{11}$	$\displaystyle = \partial_{1}{u}_{1} + k_{2}u_{2}$	(6.42)
$\displaystyle => (\epsilon_{11})_{i,j}^C$	$\displaystyle = \frac{u_{i+1,j}-u_{i,j}}{\Delta{x}_{i,j}^{F}} + k_{2,i,j}^{C}\frac{v_{i,j+1}+v_{i,j}}{2}$
$\displaystyle \dot{\epsilon}_{22}$	$\displaystyle = \partial_{2}{u}_{2} + k_{1}u_{1}$	(6.43)
$\displaystyle => (\epsilon_{22})_{i,j}^C$	$\displaystyle = \frac{v_{i,j+1}-v_{i,j}}{\Delta{y}_{i,j}^{F}} + k_{1,i,j}^{C}\frac{u_{i+1,j}+u_{i,j}}{2}$
$\displaystyle \dot{\epsilon}_{12} = \dot{\epsilon}_{21}$	$\displaystyle = \frac{1}{2}\biggl( \partial_{1}{u}_{2} + \partial_{2}{u}_{1} - k_{1}u_{2} - k_{2}u_{1} \biggr)$	(6.44)
$\displaystyle => (\epsilon_{12})_{i,j}^Z$	$\displaystyle = \frac{1}{2} \biggl( \frac{v_{i,j}-v_{i-1,j}}{\Delta{x}_{i,j}^V} + \frac{u_{i,j}-u_{i,j-1}}{\Delta{y}_{i,j}^U}$
	$\displaystyle \phantom{=\frac{1}{2}\biggl(} - k_{1,i,j}^{Z}\frac{v_{i,j}+v_{i-1,j}}{2} - k_{2,i,j}^{Z}\frac{u_{i,j}+u_{i,j-1}}{2} \biggr),$

so that the diagonal terms of the strain rate tensor are naturally defined at C-points and the symmetric off-diagonal term at Z-points. No-slip boundary conditions ( $u_{i,j-1}+u_{i,j}=0$ and $v_{i-1,j}+v_{i,j}=0$ across boundaries) are implemented via ``ghost-points''; for free slip boundary conditions $(\epsilon_{12})^Z=0$ on boundaries.

For a spherical polar grid, the coefficients of the metric terms are $k_{1}=0$ and $k_{2}=-\tan\phi/a$ , with the spherical radius and the latitude $\phi$ ; $\Delta{x}_1 = \Delta{x} = a\cos\phi \Delta\lambda$ , and $\Delta{x}_2 = \Delta{y}=a\Delta\phi$ . For a general orthogonal curvilinear grid, $k_{1}$ and $k_{2}$ can be approximated by finite differences of the cell widths:

$\displaystyle k_{1,i,j}^{C}$	$\displaystyle = \frac{1}{\Delta{y}_{i,j}^{F}} \frac{\Delta{y}_{i+1,j}^{G}-\Delta{y}_{i,j}^{G}}{\Delta{x}_{i,j}^{F}}$	(6.45)
$\displaystyle k_{2,i,j}^{C}$	$\displaystyle = \frac{1}{\Delta{x}_{i,j}^{F}} \frac{\Delta{x}_{i,j+1}^{G}-\Delta{x}_{i,j}^{G}}{\Delta{y}_{i,j}^{F}}$	(6.46)
$\displaystyle k_{1,i,j}^{Z}$	$\displaystyle = \frac{1}{\Delta{y}_{i,j}^{U}} \frac{\Delta{y}_{i,j}^{C}-\Delta{y}_{i-1,j}^{C}}{\Delta{x}_{i,j}^{V}}$	(6.47)
$\displaystyle k_{2,i,j}^{Z}$	$\displaystyle = \frac{1}{\Delta{x}_{i,j}^{V}} \frac{\Delta{x}_{i,j}^{C}-\Delta{x}_{i,j-1}^{C}}{\Delta{y}_{i,j}^{U}}$	(6.48)

The stress tensor is given by the constitutive viscous-plastic relation $\sigma_{\alpha\beta} = 2\eta\dot{\epsilon}_{\alpha\beta} + [(\zeta-\eta)\dot{\epsilon}_{\gamma\gamma} - P/2 ]\delta_{\alpha\beta}$ [Hibler, 1979]. The stress tensor divergence $(\nabla\sigma)_{\alpha} = \partial_\beta\sigma_{\beta\alpha}$ , is discretized in finite volumes. This conveniently avoids dealing with further metric terms, as these are ``hidden'' in the differential cell widths. For the -equation ( $\alpha=1$ ) we have:

$\displaystyle (\nabla\sigma)_{1}: \phantom{=}$	$\displaystyle \frac{1}{A_{i,j}^w} \int_{\mathrm{cell}}(\partial_1\sigma_{11}+\partial_2\sigma_{21})\,dx_1\,dx_2$	(6.49)
$\displaystyle =$	$\displaystyle \frac{1}{A_{i,j}^w} \biggl\{ \int_{x_2}^{x_2+\Delta{x}_2}\sigma_{... ...+\Delta{x}_1}\sigma_{21}dx_1\biggl\vert _{x_{2}}^{x_{2}+\Delta{x}_{2}} \biggr\}$
$\displaystyle \approx$	$\displaystyle \frac{1}{A_{i,j}^w} \biggl\{ \Delta{x}_2\sigma_{11}\biggl\vert _{... ...1}} + \Delta{x}_1\sigma_{21}\biggl\vert _{x_{2}}^{x_{2}+\Delta{x}_{2}} \biggr\}$
$\displaystyle =$	$\displaystyle \frac{1}{A_{i,j}^w} \biggl\{ (\Delta{x}_2\sigma_{11})_{i,j}^C - (\Delta{x}_2\sigma_{11})_{i-1,j}^C$
with
	$\displaystyle \phantom{\frac{1}{A_{i,j}^w} \biggl\{} + (\Delta{x}_1\sigma_{21})... ...Z - (\Delta{x}_1\sigma_{21})_{i,j}^Z \biggr\}(\Delta{x}_2\sigma_{11})_{i,j}^C =$	$\displaystyle \phantom{+} \Delta{y}_{i,j}^{F}(\zeta + \eta)^{C}_{i,j} \frac{u_{i+1,j}-u_{i,j}}{\Delta{x}_{i,j}^{F}}$
	$\displaystyle + \Delta{y}_{i,j}^{F}(\zeta + \eta)^{C}_{i,j} k_{2,i,j}^C \frac{v_{i,j+1}+v_{i,j}}{2}$
	$\displaystyle + \Delta{y}_{i,j}^{F}(\zeta - \eta)^{C}_{i,j} \frac{v_{i,j+1}-v_{i,j}}{\Delta{y}_{i,j}^{F}}$
	$\displaystyle + \Delta{y}_{i,j}^{F}(\zeta - \eta)^{C}_{i,j} k_{1,i,j}^{C}\frac{u_{i+1,j}+u_{i,j}}{2}$
	$\displaystyle - \Delta{y}_{i,j}^{F} \frac{P}{2}$
$\displaystyle (\Delta{x}_1\sigma_{21})_{i,j}^Z =$	$\displaystyle \phantom{+} \Delta{x}_{i,j}^{V}\overline{\eta}^{Z}_{i,j} \frac{u_{i,j}-u_{i,j-1}}{\Delta{y}_{i,j}^{U}}$	(6.50)
	$\displaystyle + \Delta{x}_{i,j}^{V}\overline{\eta}^{Z}_{i,j} \frac{v_{i,j}-v_{i-1,j}}{\Delta{x}_{i,j}^{V}}$
	$\displaystyle - \Delta{x}_{i,j}^{V}\overline{\eta}^{Z}_{i,j} k_{2,i,j}^{Z}\frac{u_{i,j}+u_{i,j-1}}{2}$
	$\displaystyle - \Delta{x}_{i,j}^{V}\overline{\eta}^{Z}_{i,j} k_{1,i,j}^{Z}\frac{v_{i,j}+v_{i-1,j}}{2}$

Similarly, we have for the -equation ( $\alpha=2$ ):

$\displaystyle (\nabla\sigma)_{2}: \phantom{=}$	$\displaystyle \frac{1}{A_{i,j}^s} \int_{\mathrm{cell}}(\partial_1\sigma_{12}+\partial_2\sigma_{22})\,dx_1\,dx_2$	(6.51)
$\displaystyle =$	$\displaystyle \frac{1}{A_{i,j}^s} \biggl\{ \int_{x_2}^{x_2+\Delta{x}_2}\sigma_{... ...+\Delta{x}_1}\sigma_{22}dx_1\biggl\vert _{x_{2}}^{x_{2}+\Delta{x}_{2}} \biggr\}$
$\displaystyle \approx$	$\displaystyle \frac{1}{A_{i,j}^s} \biggl\{ \Delta{x}_2\sigma_{12}\biggl\vert _{... ...1}} + \Delta{x}_1\sigma_{22}\biggl\vert _{x_{2}}^{x_{2}+\Delta{x}_{2}} \biggr\}$
$\displaystyle =$	$\displaystyle \frac{1}{A_{i,j}^s} \biggl\{ (\Delta{x}_2\sigma_{12})_{i+1,j}^Z - (\Delta{x}_2\sigma_{12})_{i,j}^Z$
with
	$\displaystyle \phantom{\frac{1}{A_{i,j}^s} \biggl\{} + (\Delta{x}_1\sigma_{22})... ...- (\Delta{x}_1\sigma_{22})_{i,j-1}^C \biggr\}(\Delta{x}_1\sigma_{12})_{i,j}^Z =$	$\displaystyle \phantom{+} \Delta{y}_{i,j}^{U}\overline{\eta}^{Z}_{i,j} \frac{u_{i,j}-u_{i,j-1}}{\Delta{y}_{i,j}^{U}}$
	$\displaystyle + \Delta{y}_{i,j}^{U}\overline{\eta}^{Z}_{i,j} \frac{v_{i,j}-v_{i-1,j}}{\Delta{x}_{i,j}^{V}}$
	$\displaystyle - \Delta{y}_{i,j}^{U}\overline{\eta}^{Z}_{i,j} k_{2,i,j}^{Z}\frac{u_{i,j}+u_{i,j-1}}{2}$
	$\displaystyle - \Delta{y}_{i,j}^{U}\overline{\eta}^{Z}_{i,j} k_{1,i,j}^{Z}\frac{v_{i,j}+v_{i-1,j}}{2}$
$\displaystyle (\Delta{x}_2\sigma_{22})_{i,j}^C =$	$\displaystyle \phantom{+} \Delta{x}_{i,j}^{F}(\zeta - \eta)^{C}_{i,j} \frac{u_{i+1,j}-u_{i,j}}{\Delta{x}_{i,j}^{F}}$
	$\displaystyle + \Delta{x}_{i,j}^{F}(\zeta - \eta)^{C}_{i,j} k_{2,i,j}^{C} \frac{v_{i,j+1}+v_{i,j}}{2}$
	$\displaystyle + \Delta{x}_{i,j}^{F}(\zeta + \eta)^{C}_{i,j} \frac{v_{i,j+1}-v_{i,j}}{\Delta{y}_{i,j}^{F}}$
	$\displaystyle + \Delta{x}_{i,j}^{F}(\zeta + \eta)^{C}_{i,j} k_{1,i,j}^{C}\frac{u_{i+1,j}+u_{i,j}}{2}$
	$\displaystyle -\Delta{x}_{i,j}^{F} \frac{P}{2}$

Again, no slip boundary conditions are realized via ghost points and $u_{i,j-1}+u_{i,j}=0$ and $v_{i-1,j}+v_{i,j}=0$ across boundaries. For free slip boundary conditions the lateral stress is set to zeros. In analogy to $(\epsilon_{12})^Z=0$ on boundaries, we set $\sigma_{21}^{Z}=0$ , or equivalently $\eta_{i,j}^{Z}=0$ , on boundaries.

6.6.2.4.3 Thermodynamics

In its original formulation the sea ice model [Menemenlis et al., 2005] uses simple thermodynamics following the appendix of Semtner [1976]. This formulation does not allow storage of heat, that is, the heat capacity of ice is zero. Upward conductive heat flux is parameterized assuming a linear temperature profile and together with a constant ice conductivity. It is expressed as $(K/h)(T_{w}-T_{0})$ , where is the ice conductivity, the ice thickness, and $T_{w}-T_{0}$ the difference between water and ice surface temperatures. This type of model is often refered to as a ``zero-layer'' model. The surface heat flux is computed in a similar way to that of Parkinson and Washington [1979] and Manabe et al. [1979].

The conductive heat flux depends strongly on the ice thickness . However, the ice thickness in the model represents a mean over a potentially very heterogeneous thickness distribution. In order to parameterize a sub-grid scale distribution for heat flux computations, the mean ice thickness is split into seven thickness categories $H_{n}$ that are equally distributed between and a minimum imposed ice thickness of cm by $H_n= \frac{2n-1}{7}\,h$ for $n\in[1,7]$ . The heat fluxes computed for each thickness category is area-averaged to give the total heat flux [Hibler, 1984]. To use this thickness category parameterization set #define SEAICE_MULTICATEGORY; note that this requires different restart files and switching this flag on in the middle of an integration is not possible.

The atmospheric heat flux is balanced by an oceanic heat flux from below. The oceanic flux is proportional to $\rho\,c_{p}\left(T_{w}-T_{fr}\right)$ where $\rho$ and $c_{p}$ are the density and heat capacity of sea water and $T_{fr}$ is the local freezing point temperature that is a function of salinity. This flux is not assumed to instantaneously melt or create ice, but a time scale of three days (run-time parameter SEAICE_gamma_t) is used to relax $T_{w}$ to the freezing point. The parameterization of lateral and vertical growth of sea ice follows that of Hibler [1980,1979]; the so-called lead closing parameter $h_{0}$ (run-time parameter HO) has a default value of 0.5 meters.

On top of the ice there is a layer of snow that modifies the heat flux and the albedo [Zhang et al., 1998]. Snow modifies the effective conductivity according to

$\displaystyle \frac{K}{h} \rightarrow \frac{1}{\frac{h_{s}}{K_{s}}+\frac{h}{K}},$

where

is the conductivity of snow and

the snow thickness. If enough snow accumulates so that its weight submerges the ice and the snow is flooded, a simple mass conserving parameterization of snowice formation (a flood-freeze algorithm following Archimedes' principle) turns snow into ice until the ice surface is back at

[Leppäranta, 1983]. The flood-freeze algorithm is enabled with the CPP-flag SEAICE_ALLOW_FLOODING and turned on with run-time parameter SEAICEuseFlooding=.true..

Effective ice thickness (ice volume per unit area, $c\cdot{h}$ ), concentration and effective snow thickness ( $c\cdot{h}_{s}$ ) are advected by ice velocities:

$\displaystyle \frac{\partial{X}}{\partial{t}} = - \nabla\cdot\left(\ensuremath{\vec{\mathbf{u}}}\,X\right) + \Gamma_{X} + D_{X}$

(6.52)

where $\Gamma_X$ are the thermodynamic source terms and $D_{X}$ the diffusive terms for quantities $X=(c\cdot{h}), c, (c\cdot{h}_{s})$ . From the various advection scheme that are available in the MITgcm, we choose flux-limited schemes [multidimensional 2nd and 3rd-order advection scheme with flux limiter Hundsdorfer and Trompert, 1994; Roe, 1985] to preserve sharp gradients and edges that are typical of sea ice distributions and to rule out unphysical over- and undershoots (negative thickness or concentration). These scheme conserve volume and horizontal area and are unconditionally stable, so that we can set $D_{X}=0$ . Run-timeflags: SEAICEadvScheme (default=2), DIFF1 (default=0.004).

There is considerable doubt about the reliability of a ``zero-layer'' thermodynamic model -- Semtner [1984] found significant errors in phase (one month lead) and amplitude ( $\approx$ 50%overestimate) in such models -- so that today many sea ice models employ more complex thermodynamics. The MITgcm sea ice model provides the option to use the thermodynamics model of Winton [2000], which in turn is based on the 3-layer model of Semtner [1976] and which treats brine content by means of enthalpy conservation. This scheme requires additional state variables, namely the enthalpy of the two ice layers (instead of effective ice salinity), to be advected by ice velocities. The internal sea ice temperature is inferred from ice enthalpy. To avoid unphysical (negative) values for ice thickness and concentration, a positive 2nd-order advection scheme with a SuperBee flux limiter [Roe, 1985] is used in this study to advect all sea-ice-related quantities of the Winton [2000] thermodynamic model. Because of the non-linearity of the advection scheme, care must be taken in advecting these quantities: when simply using ice velocity to advect enthalpy, the total energy (i.e., the volume integral of enthalpy) is not conserved. Alternatively, one can advect the energy content (i.e., product of ice-volume and enthalpy) but then false enthalpy extrema can occur, which then leads to unrealistic ice temperature. In the currently implemented solution, the sea-ice mass flux is used to advect the enthalpy in order to ensure conservation of enthalpy and to prevent false enthalpy extrema.

6.6.2.5 Key subroutines

Top-level routine: seaice_model.F

C     !CALLING SEQUENCE:
c ...
c  seaice_model (TOP LEVEL ROUTINE)
c  |
c  |-- #ifdef SEAICE_CGRID
c  |     SEAICE_DYNSOLVER
c  |     |
c  |     |-- < compute proxy for geostrophic velocity >
c  |     |
c  |     |-- < set up mass per unit area and Coriolis terms >
c  |     |
c  |     |-- < dynamic masking of areas with no ice >
c  |     |
c  |     |

c  |   #ELSE
c  |     DYNSOLVER
c  |   #ENDIF
c  |
c  |-- if ( useOBCS ) 
c  |     OBCS_APPLY_UVICE
c  |
c  |-- if ( SEAICEadvHeff .OR. SEAICEadvArea .OR. SEAICEadvSnow .OR. SEAICEadvSalt )
c  |     SEAICE_ADVDIFF
c  |
c  |-- if ( usePW79thermodynamics ) 
c  |     SEAICE_GROWTH
c  |
c  |-- if ( useOBCS ) 
c  |     if ( SEAICEadvHeff ) OBCS_APPLY_HEFF
c  |     if ( SEAICEadvArea ) OBCS_APPLY_AREA
c  |     if ( SEAICEadvSALT ) OBCS_APPLY_HSALT
c  |     if ( SEAICEadvSNOW ) OBCS_APPLY_HSNOW
c  |
c  |-- < do various exchanges >
c  |
c  |-- < do additional diagnostics >
c  |
c  o

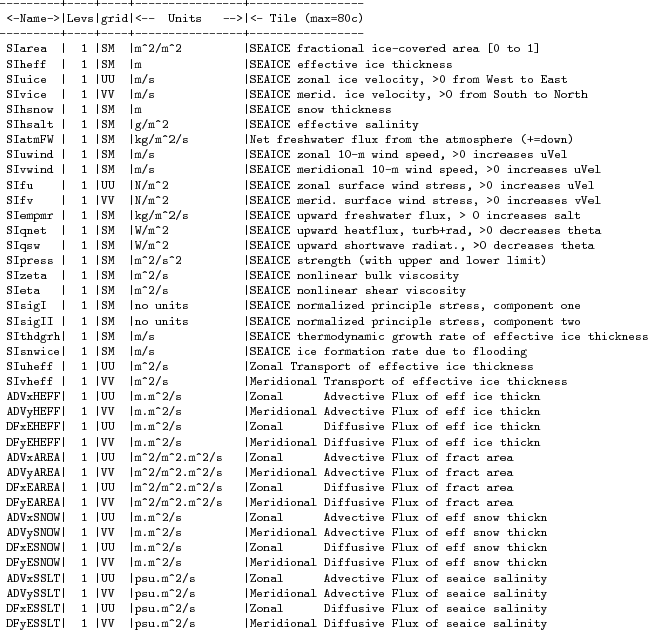
6.6.2.6 SEAICE diagnostics

Diagnostics output is available via the diagnostics package (see Section 7.1). Available output fields are summarized in Table 6.6.2.6.

**Table 6.18:** Available diagnostics of the seaice-package
$\begin{table}\centering {\footnotesize \begin{verbatim}---------+----+----+---... ... \vert Meridional Diffusive Flux of seaice salinity\end{verbatim} }\end{table}$

6.6.2.7 Experiments and tutorials that use seaice

Labrador Sea experiment in lab_sea verification directory.

Next: 6.6.3 SHELFICE Package Up: 6.6 Sea Ice Packages Previous: 6.6.1 THSICE: The Thermodynamic Contents

mitgcm-support@mitgcm.org

Last update 2011-01-09