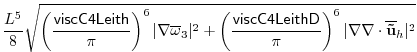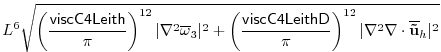|
 |
|||||||||||
 |
|
|||||||||||
 |
 |
|||||||||||
|
Next: 2.21.2 Mercator, Nondimensional Equations Up: 2.21 Nonlinear Viscosities for Previous: 2.21 Nonlinear Viscosities for Contents Subsections
2.21.1 Eddy ViscosityA turbulent closure provides an approximation to the 'eddy' terms on the right of the preceding equations. The simplest form of LES is just to increase the viscosity and diffusivity until the viscous and diffusive scales are resolved. That is, we approximate:
2.21.1.1 Reynolds-Number Limited Eddy ViscosityOne way of ensuring that the gridscale is sufficiently viscous (ie. resolved) is to choose the eddy viscosity
MITgcm users can select horizontal eddy viscosities based on
While it is certainly necessary that viscosity be active at the
gridscale, the wavelength where dissipation of energy or enstrophy
occurs is not necessarily
2.21.1.2 Vertical Eddy ViscositiesVertical eddy viscosities are often chosen in a more subjective way, as model stability is not usually as sensitive to vertical viscosity. Usually the 'observed' value from finescale measurements, etc., is used (eg. viscAr
2.21.1.3 Smagorinsky ViscositySome Smagorinsky [1963,1993] suggest choosing a viscosity that depends on the resolved motions. Thus, the overall viscous operator has a nonlinear dependence on velocity. Smagorinsky chose his form of viscosity by considering Kolmogorov's ideas about the energy spectrum of 3-d isotropic turbulence.
Kolmogorov suppposed that is that energy is injected into the flow at
large scales (small
There are two methods of ensuring that the Kolmogorov length is
resolved in MITgcm. 1) The user can estimate the flux of energy
through spectral space for a given simulation and adjust grid spacing
or viscAh to ensure that
Smagorinsky formed the energy equation from the momentum equations by
dotting them with velocity. There are some complications when using
the hydrostatic approximation as described by Smagorinsky
Smagorinsky [1993]. The positive definite energy dissipation by
horizontal viscosity in a hydrostatic flow is
To make
Where the deformation rate appropriate for hydrostatic flows with shallow-water scaling is
The coefficient viscC2Smag is what an MITgcm user sets, and it replaces the proportionality in the Kolmogorov length with an equality. Others Griffies and Hallberg [2000b] suggest values of viscC2Smag from 2.2 to 4 for oceanic problems. Smagorinsky Smagorinsky [1993] shows that values from 0.2 to 0.9 have been used in atmospheric modeling. Smagorinsky Smagorinsky [1993] shows that a corresponding vertical viscosity should be used:
This vertical viscosity is currently not implemented in MITgcm (although it may be soon).
2.21.1.4 Leith ViscosityLeith Leith [1968,1996] notes that 2-d turbulence is quite different from 3-d. In two-dimensional turbulence, energy cascades to larger scales, so there is no concern about resolving the scales of energy dissipation. Instead, another quantity, enstrophy, (which is the vertical component of vorticity squared) is conserved in 2-d turbulence, and it cascades to smaller scales where it is dissipated.
Following a similar argument to that above about energy flux, the
enstrophy flux is estimated to be equal to the positive-definite
gridscale dissipation rate of enstrophy
2.21.1.5 Modified Leith ViscosityThe argument above for the Leith viscosity parameterization uses concepts from purely 2-dimensional turbulence, where the horizontal flow field is assumed to be divergenceless. However, oceanic flows are only quasi-two dimensional. While the barotropic flow, or the flow within isopycnal layers may behave nearly as two-dimensional turbulence, there is a possibility that these flows will be divergent. In a high-resolution numerical model, these flows may be substantially divergent near the grid scale, and in fact, numerical instabilities exist which are only horizontally divergent and have little vertical vorticity. This causes a difficulty with the Leith viscosity, which can only responds to buildup of vorticity at the grid scale.
MITgcm offers two options for dealing with this problem. 1) The
Smagorinsky viscosity can be used instead of Leith, or in conjunction
with Leith-a purely divergent flow does cause an increase in
Smagorinsky viscosity. 2) The viscC2LeithD parameter can be
set. This is a damping specifically targeting purely divergent
instabilities near the gridscale. The combined viscosity has the
form:
Whether there is any physical rationale for this correction is unclear at the moment, but the numerical consequences are good. The divergence in flows with the grid scale larger or comparable to the Rossby radius is typically much smaller than the vorticity, so this adjustment only rarely adjusts the viscosity if
2.21.1.6 Courant-Freidrichs-Lewy Constraint on ViscosityWhatever viscosities are used in the model, the choice is constrained by gridscale and timestep by the Courant-Freidrichs-Lewy (CFL) constraint on stability:
The viscosities may be automatically limited to be no greater than these values in MITgcm by specifying viscAhGridMax
Following Griffies and Hallberg [2000b], we note that there is a factor of
2.21.1.7 Biharmonic ViscosityHolland [1978] suggested that eddy viscosities ought to be focuses on the dynamics at the grid scale, as larger motions would be 'resolved'. To enhance the scale selectivity of the viscous operator, he suggested a biharmonic eddy viscosity instead of a harmonic (or Laplacian) viscosity:Griffies and Hallberg [2000b] propose that if one scales the biharmonic viscosity by stability considerations, then the biharmonic viscous terms will be similarly active to harmonic viscous terms at the gridscale of the model, but much less active on larger scale motions. Similarly, a biharmonic diffusivity can be used for less diffusive flows. In practice, biharmonic viscosity and diffusivity allow a less viscous, yet numerically stable, simulation than harmonic viscosity and diffusivity. However, there is no physical rationale for such operators being of leading order, and more boundary conditions must be specified than for the harmonic operators. If one considers the approximations of 2.208 and 2.219 to be terms in the Taylor series expansions of the eddy terms as functions of the large-scale gradient, then one can argue that both harmonic and biharmonic terms would occur in the series, and the only question is the choice of coefficients. Using biharmonic viscosity alone implies that one zeros the first non-vanishing term in the Taylor series, which is unsupported by any fluid theory or observation.
Nonetheless, MITgcm supports a plethora of biharmonic viscosities
and diffusivities, which are controlled with parameters named
similarly to the harmonic viscosities and diffusivities with the
substitution
However, it should be noted that unlike the harmonic forms, the biharmonic scaling does not easily relate to whether energy-dissipation or enstrophy-dissipation scales are resolved. If similar arguments are used to estimate these scales and scale them to the gridscale, the resulting biharmonic viscosities should be:
Thus, the biharmonic scaling suggested by Griffies and Hallberg [2000b] implies:
It is not at all clear that these assumptions ought to hold. Only the Griffies and Hallberg [2000b] forms are currently implemented in MITgcm.
2.21.1.8 Selection of Length ScaleAbove, the length scale of the grid has been denoted
Next: 2.21.2 Mercator, Nondimensional Equations Up: 2.21 Nonlinear Viscosities for Previous: 2.21 Nonlinear Viscosities for Contents mitgcm-support@mitgcm.org |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



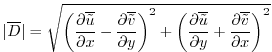
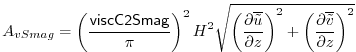
![$\displaystyle \sqrt{\left[{\frac{\partial{\ }}{\partial{x}}}
\left({\frac{\par...
...{x}}}
-{\frac{\partial{\overline{{\tilde u}} }}{\partial{y}}}\right)\right]^2}$](img1048.png)
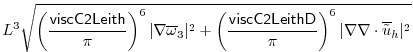
![$\displaystyle \sqrt{\left[{\frac{\partial{\ }}{\partial{x}}}\left({\frac{\parti...
...{x}}}
+{\frac{\partial{\overline{{\tilde v}} }}{\partial{y}}}\right)\right]^2}$](img1051.png)