Planet-in-a-Bottle
story by Helen HillHere we look at work by Sai Ravela, John Marshall, Chris Hill, Andrew Wong and Scott Stransky in which they use MITgcm to provide the virtual analogue for a fluid lab experiment in the physical laboratory, as part of an effort to demonstrate how to achieve real-time model-data synthesis, using measurements from a robotically controlled automated sensor system.
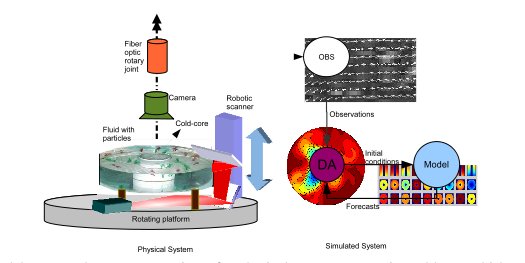
Figure 1. The components of the system: The laboratory observatory consists of a physical system: a rotating table on which a tank, camera and control system for illumination are mounted. The computational part consists of a measurement system for velocimetry, a numerical model (MITgcm), and an assimilation system.
This project combines four things:
-
A differentially heated, rotating annulus experiment in the lab.
-
A numerical analogue of the lab experiment – using MITgcm.
-
An observing system supplying a digital feed of the lab fluid state.
-
A data assimilation harness that keeps the numerical model consistent with its laboratory counterpart.
The Laboratory Experiment.
The differentially-heated rotating annulus experiment is both a direct analogue of the planetary wave problem (Hide, 1967) and a convenient vehicle for studying many aspects of baroclinic instability. When the center of a spinning annulus is cooled, the water adjacent to the cooling becomes dense and sinks. In response, warmer water moves in from the periphery and an overturning circulation is established. As can be clearly observed in the movie below, at moderately strong temperature gradients and rotation rates the circulation develops in to a rich 3-dimensional pattern of eddies and jets evocative of similar structures observed in the atmosphere and oceans.
The Numerical Simulation.
The team uses the MITgcm to solve the equations of an incompressible Boussinesq fluid in hydrostatic balance that provide a numerical analogue of the lab experiment. Finite volume forms of the governing equations are solved in cylindrical polar coordinates within a domain of inner radius 8cm and outer radius 45cm divided into 23 radial bins (1cm/bin) and 120 azimuthal bins (3° bins). The vertical coordinate is discretized using 15 levels non-uniformly distributed over the 15cm depth of fluid. Momentum equations are stepped forward using a second-order Adams Bashforth technique. Theta is advected with an upwind-biased direct space-time technique using a Sweby flux-limiter. The treatment of vertical transport is implicit. A 2-d equation for the surface pressure field is solved at each timestep using a conjugate gradient method ensuring that the flow remains non-divergent.
The model is initialised with a uniform temperature field to which a small random component is added to initiate hydrodynamic instability. This instability grows, producing a circulation that is typically different from the physical simulation.
The videos below show surface and vertical temperature field evolution from the (unconstrained) MITgcm simulation.
The model performs in better than realtime. On one processor of an Altix350, the team is able to carry out a 10 second simulation in 8 seconds.
The Observing System.
The fluid is contained in a cylindrical plexiglass tank mounted on a rotating platform. A robotic arm (the “Z-arm”) moves a mirror up and down to position a horizontal sheet of laser light at any depth in the fluid. Neutrally buoyant fluorescent particles respond to incident laser illumination and appear as texture. Images are transferred out of the rotating frame via a fiber-optic rotary joint.
A physical simulation begins when the rotating table is spun-up to a desired rotation (typically 2 Π/6 rad s-1). Once the fluid is in solid body rotation, a chiller cools the core and a temperature differential is set up across the annulus. In around 5 minutes, thermally-induced instabilities cascade in to a wave-like circulation evocative of planetary circulations.
The laser is then turned on and velocity is computed in under a second per image pair acquired at a fluid level. The maximum velocity is of the order of 2cm/s. Observations are gathered repeatedly over five evenly-spaced levels in the fluid, in a cycle time of 5 seconds. It is these observations that are used to constrain the numerical model.
The above video, which has an audio component, shows the mirror moving through the volume taking measurements at five layers. Each scan takes approximately 5 seconds to complete.
The above video shows the camera’s view of illuminated particles at a chosen level of the fluid in the rotating frame. Particles can be observed (albeit at low resolution) to move with the flow in eddies and vortices. The green arrows indicate real-time velocity vectors. The yellow arrows (overlayed during the last part of the video) show the unconstrained model vectors. Both vectors are plotted to the same scale (~2cm/s).
The Assimilation Scheme.
The hybrid filter uses a flow-free update (initialization) that is deterministic, and a flow-dependent (tracking) update based on an ensemble in a successive uncertainty reduction scheme. In both cases, states are estimated at observed layers and interpolated to the unobserved ones using functions learned from forecasts. In the flow-free update, an isotropic Gaussian is used to capture spatial correlations. In the flow-dependent update, snapshots of boundary-conditions perturbed simulations are used to capture uncertainty. Localization is used in both cases with overlapping spatial contexts.
Putting it all Together: The System in Action.
This video shows the model velocities being constrained by observed velocities, depicted for a single ensemble member at a single horizontal layer of the fluid. The video shows model velocity vectors on the right as the model spins up (00:00 – 00:04s of video time) to roughly 200s of simulation. The first set of observations are encountered, vectors flash on the left panel of video, and the model field immediately adjusts. At the next time step, observations are no longer available, and the panel on the left becomes “blank.” As time progresses, forecast model velocities are shown on the right and updated every second of simulation time. After 10-model seconds (00:10s mark on video time), new observations are available, and the model adjusts itself again. In this way, the forecast, assimilate cycle continues.
Over time, one can observe that the model vectors become consistent with the observations. Notice that these adjustments are robust in the presence of observation noise, and that the model fills in a circulation, where one is not present in the observations, in a manner consistent with the large-scale circulation. By the end of the estimation sequence, the model is nicely registered to observations.
Want to know more? Contact Sai
References:
Hide, R. Theory of axisymmetric thermal convection in a rotating fluid annulus, Phys. Fluids., 10, 56-58, 1967.
Ravela, S., J. Marshall, C. Hill, A. Wong and S. Stransky (2009) A Real-time Observatory for Laboratory Simulation of Planetary Flows, Experiments in Fluids, DOI:10.1007/s00348-009-0752-0


